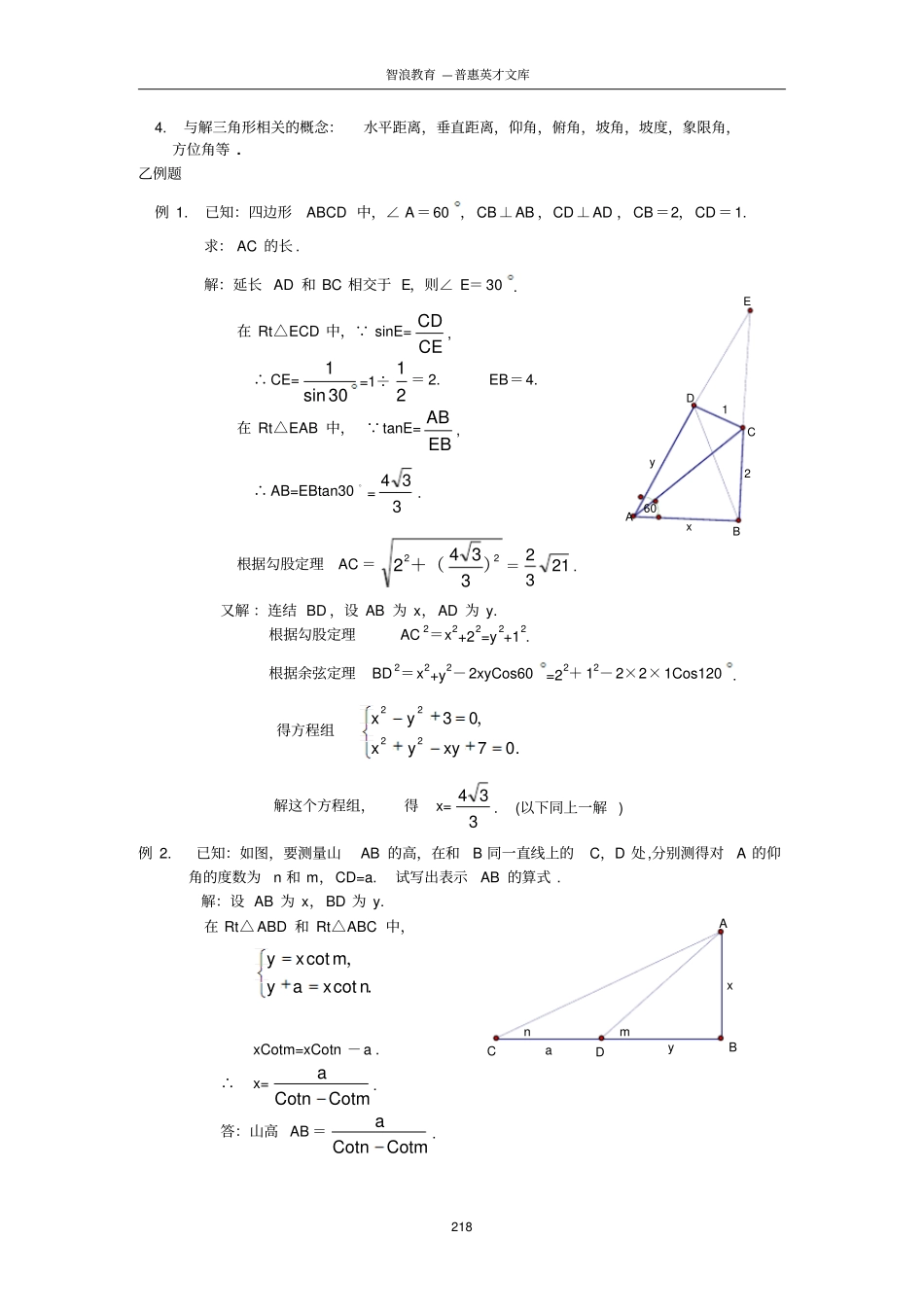
智浪教育—普惠英才文库217初中数学竞赛辅导资料解三角形甲内容提要1.由三角形的已知元素,求出所有未知元素的过程叫做解三角形.2.解直角三角形所根据的定理(在Rt△ABC中,∠C=Rt∠).①边与边的关系:勾股定理----――c2=a2+b2.②角与角的关系:两个锐角互余----∠A+∠B=Rt∠③边与角的关系:(锐角三角函数定义)SinA=ca,CosA=cb,tanA=ba,CotA=ab.④互余的两个角的三角函数的关系:Sin(90-A)=CosA,Cos(90-A)=SinA,tan(90-A)=CotA,Cot(90-A)=tanA.⑤特殊角的三角函数值:角A的度数030456090SinA的值02122231CosA的值12322210tanA的值03313不存在CotA的值不存在31330锐角的正弦、正切随着角度的增大而增大(即增函数);余弦、余切随着角度的增大而减小(即减函数).3.解斜三角形所根据的定理(在△ABC中)①正弦定理:SinCcSinBbSinAa=2R.(R是△ABC外接圆半径).②余弦定理:c2=a2+b2-2abCosC;b2=c2+a2-2caCosB;a2=c2+b2-2cbCosA.③互补的两个角的三角函数的关系:Sin(180-A)=sinA,Cos(180-A)=-cosA,tan(180-A)=-cotA,cotA(180-A)=-tanA.④S△ABC=21absinC=21bcsinA=21casinB.cbaABC智浪教育—普惠英才文库2184.与解三角形相关的概念:水平距离,垂直距离,仰角,俯角,坡角,坡度,象限角,方位角等.乙例题例1.已知:四边形ABCD中,∠A=60,CB⊥AB,CD⊥AD,CB=2,CD=1.求:AC的长.解:延长AD和BC相交于E,则∠E=30.在Rt△ECD中, sinE=CECD,∴CE=30sin1=1÷21=2.EB=4.在Rt△EAB中, tanE=EBAB,∴AB=EBtan30。=334.根据勾股定理AC=223342)+(=2132.又解:连结BD,设AB为x,AD为y.根据勾股定理AC2=x2+22=y2+12.根据余弦定理BD2=x2+y2-2xyCos60=22+12-2×2×1Cos120.得方程组.07032222xyyxyx,解这个方程组,得x=334.(以下同上一解)例2.已知:如图,要测量山AB的高,在和B同一直线上的C,D处,分别测得对A的仰角的度数为n和m,CD=a.试写出表示AB的算式.解:设AB为x,BD为y.在Rt△ABD和Rt△ABC中,.cotcotnxaymxy,xCotm=xCotn-a.∴x=CotmCotna.答:山高AB=CotmCotna.yx6012ABCDEyxanmABCD智浪教育—普惠英才文库219例3.已知:四边形ABCD中,∠ABC=135,∠BCD=120,CD=6,AB=6,BC=5-3.求:AD的长.(1991年全国初中数学联赛题)解:作AE∥BC交CD于E,BF⊥AE于F,CG⊥AE于G..在Rt△ABF中,BF=6Sin45=3,AF=BF=3.在Rt△CGE中,GE=CGtan30=3×33=1,∴CE=2,ED=4.∴AE=3+5-3+1=6,∠AED=120.在△AED中,根据余弦定理,得AD2=62+42-2×6×4Cos120=76.∴AD=219.例4.如图,要测量河对岸C,D两个目标之间的距离,在A,B两个测站,测得平面角∠CAB=30,∠CAD=45,∠DBC=75,∠DBA=45,AB=3.试求C,D的距离.解:在△ABC中, ∠ACB=∠CAB=30,∴BC=AB=3,∴AC=23cos30=3.在△ABD中,∠ADB=60由正弦定理,45sinAD=60sinAB,AD=60sinAB×sin45=3÷23×22=2.在△ACD中,由余弦定理,得CD2=32+(2)2-2×3×2Cos45=5∴CD=5.3河流75453045ABCD5-366120135ABCDEFG智浪教育—普惠英才文库220例5.已知:O是凸五边形ABCDE内的一点且∠1=∠2,∠3=∠4,∠5=∠6,∠7=∠8.求证:∠9和∠10相等或互补(1985年全国初中数学联赛题)证明:根据正弦定理,得5sin4sin3sin2sin1sin10sinOAODOCOCOBOB=9sin8sin7sin6sinOAOEOEOD.∴sin10=sin9∴∠9和∠10相等或互补.例6.已知:二次方程mx2-(m-2)x+41(m-1)=0两个不相等的实数根,恰好是直角三角形两个锐角的正弦值.求:这个直角三角形的斜边与斜边上的高的比.解:作Rt△ABC斜边上的高CD.则sinA=ACCD,sinB=BCCD. sinA和sinB是方程的两根,根据韦达定理,得sinA+sinB=mm2;(1)sinAsinB=mm41.(2)即ACCDBCCD=mm41.(3)(1)2-2(2)得:(sinA)2+(sinB)2=(mm2)2-mm21. sinB=cosA,且(sinA)2+(cosA)2=1,∴(mm2)2-mm21=1,m2+7m-8=0,∴m=1,m=-8.由(3)ACCDBCCD=ABCDABCDCD2==mm41.∴CDAB=14mm.当m=1时,没有意义;当m=-8时,CDAB=932.即直角三角形斜边与斜边上的高的比是32∶9.10987654312ABCDEOABCD智浪教育—普惠英才文库221丙练习1.填空:①如果从点A对着点B测得仰角...