北京海淀区普通中学2018届初三数学中考复习直角三角形全等的判定专项复习训练题含答案VIP免费

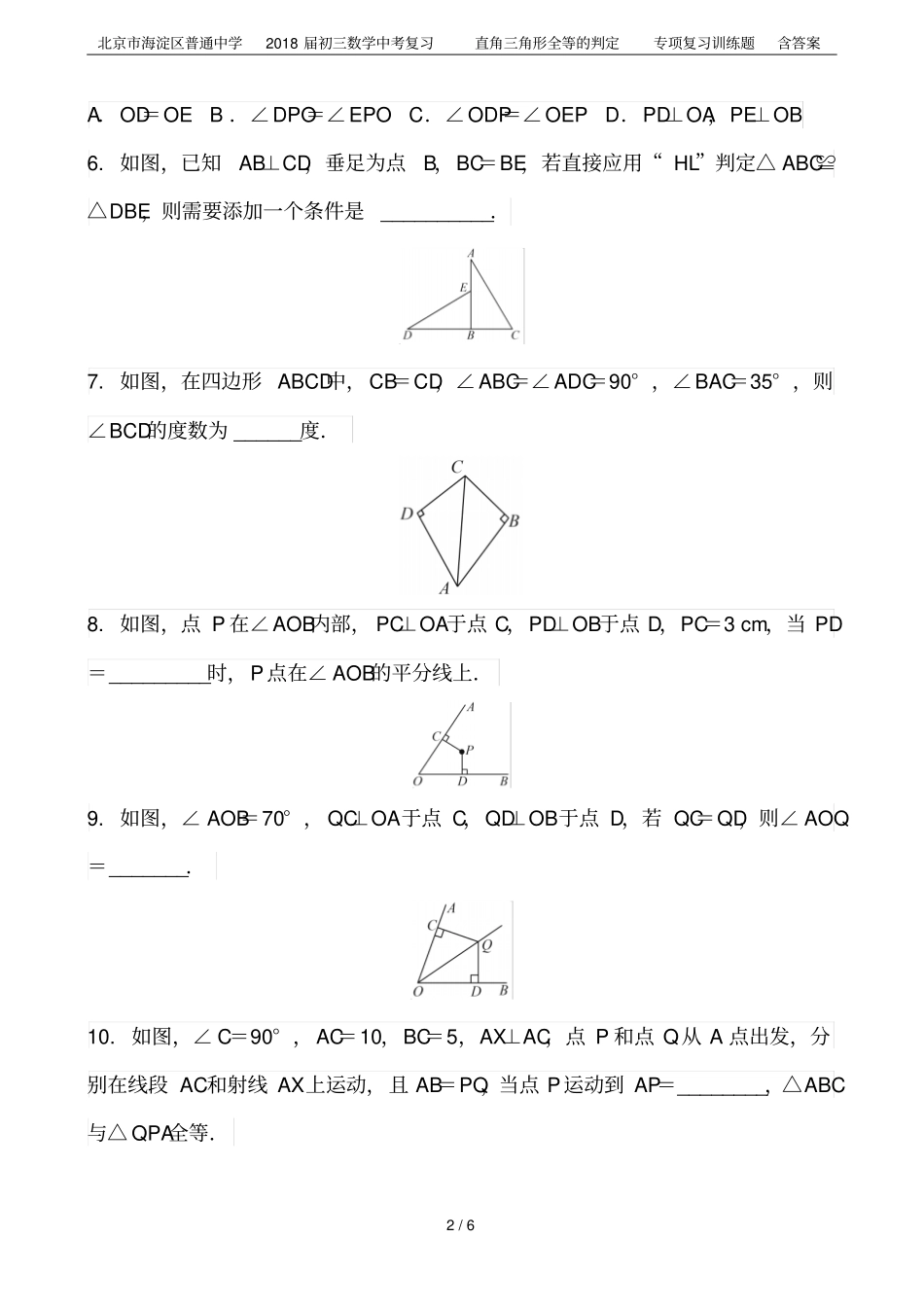
北京市海淀区普通中学2018届初三数学中考复习直角三角形全等的判定专项复习训练题含答案1/6北京市海淀区普通中学2018届初三数学中考复习直角三角形全等的判定专项复习训练题1．如图，∠BAD＝∠BCD＝90°，AB＝CB，可以证明△BAD≌△BCD的理由是()A．HLB．ASAC．SASD．AAS2．下列判定两直角三角形全等的方法，错误的是()A．两条直角边对应相等B．斜边和一直角边对应相等C．两个锐角对应相等D．斜边和一锐角对应相等3.如图，点P是AD上一点，PE⊥AC于点E，PF⊥AB于点F.若PE＝PF，∠CAD＝20°，则∠BAD＝()A．10°B．20°C．30°D．40°4.如图，在Rt△ABC中，∠BAC＝90°，DE⊥BC，AC＝6，EC＝6，∠ACB＝60°，则∠ACD的度数为()A．45°B．30°C．20°D．15°5.如图，OC是∠AOB内的一条射线，点D，P，E分别在OA，OC，OB上，且PD＝PE，结合下列条件，不能得出OC平分∠AOB的是()北京市海淀区普通中学2018届初三数学中考复习直角三角形全等的判定专项复习训练题含答案2/6A．OD＝OEB．∠DPO＝∠EPOC．∠ODP＝∠OEPD．PD⊥OA，PE⊥OB6.如图，已知AB⊥CD，垂足为点B，BC＝BE，若直接应用“HL”判定△ABC≌△DBE，则需要添加一个条件是__________．7.如图，在四边形ABCD中，CB＝CD，∠ABC＝∠ADC＝90°，∠BAC＝35°，则∠BCD的度数为______度．8.如图，点P在∠AOB内部，PC⊥OA于点C，PD⊥OB于点D，PC＝3cm，当PD＝_________时，P点在∠AOB的平分线上．9.如图，∠AOB＝70°，QC⊥OA于点C，QD⊥OB于点D，若QC＝QD，则∠AOQ＝_______．10.如图，∠C＝90°，AC＝10，BC＝5，AX⊥AC，点P和点Q从A点出发，分别在线段AC和射线AX上运动，且AB＝PQ，当点P运动到AP＝________，△ABC与△QPA全等．北京市海淀区普通中学2018届初三数学中考复习直角三角形全等的判定专项复习训练题含答案3/611.如图，△ABC的外角∠ACD的平分线CE与内角∠ABC的平分线BE交于点E，若∠BAC＝70°，则∠CAE＝_______．12.如图，∠ACB＝∠ADB＝90°，AC＝AD，点E在AB上，连结CE，DE.求证：CE＝DE.13.如图，BF⊥AC，CE⊥AB，且BD＝CD，请说明点D在∠BAC的平分线上．14.如图，P点为△ABC内一点，PA平分∠BAC，PB＝PC，求证：AB＝AC.北京市海淀区普通中学2018届初三数学中考复习直角三角形全等的判定专项复习训练题含答案4/615.如图，在△ABC中，点P在BC边的垂直平分线上，过点P分别作AB，AC(或其延长线)的垂线，垂足分别为点M，N，且MB＝NC，那么点P在∠BAC的平分线上吗？请说明理由．16.将两个全等的直角三角形ABC和DBE按图①方式摆放，其中∠ACB＝∠DEB＝90°，∠A＝∠D＝30°，点E落在AB上，DE所在直线交AC所在直线于点F.(1)求证：AF＋EF＝DE；(2)若将图①中的△DBE绕点B按顺时针方向旋转角α，且0°<α<60°，其他条件不变，请在图②中画出变换后的图形，并直接写出你在(1)中猜想的结论是否仍然成立；(3)若将图①中的△DBE绕点B按顺时针方向旋转角β，且60°<β<180°，其北京市海淀区普通中学2018届初三数学中考复习直角三角形全等的判定专项复习训练题含答案5/6他条件不变，如图③.你认为(1)中猜想的结论还成立吗？若成立，写出证明过程：若不成立，请写出AF，EF与DE之间的关系，并说明理由．答案：1---5ACBBC6.DE＝AC7.1108.3cm9.35°10.5或1011.55°12.证明：在Rt△ACB和Rt△ADB中， AC＝AD，AB＝AB，∴Rt△ACB≌Rt△ADB，∴∠1＝∠2， AC＝AD，∠1＝∠2，AE＝AE，∴△ACE≌△ADE，∴CE＝DE.13.解： BF⊥AC，CE⊥AB，∴∠DEB＝∠DFC＝90°， ∠DEB＝∠DFC，∠BDE＝∠CDF，BD＝CD，△DEB≌△DFC，∴DE＝DF， BF⊥AC，CE⊥AB，∴点D在∠北京市海淀区普通中学2018届初三数学中考复习直角三角形全等的判定专项复习训练题含答案6/6BAC的平分线上．14.证明：作PD⊥AB于点D，PE⊥AC于点E，图略． PA平分∠BAC，∴PD＝PE，又 PA＝PA，∴Rt△PAD≌Rt△PAE(HL)，∴AD＝AE，同理可证Rt△PBD≌Rt△PCE(HL)，∴BD＝CE，∴AD＋BD＝AE＋CE，即AB＝AC.15.解：点P在∠BAC的平分线上．理由：连结CP，BP，图略． 点P在BC边的垂直平分线上，∴CP＝BP，在Rt△BPM和Rt△CPN中，BP＝CP，MB＝NC，∴Rt△BPM≌Rt△CPN，∴PM＝PN， PM⊥AB，...