广东文科数学第一轮复习第11讲-零点定理与根的分布VIP免费

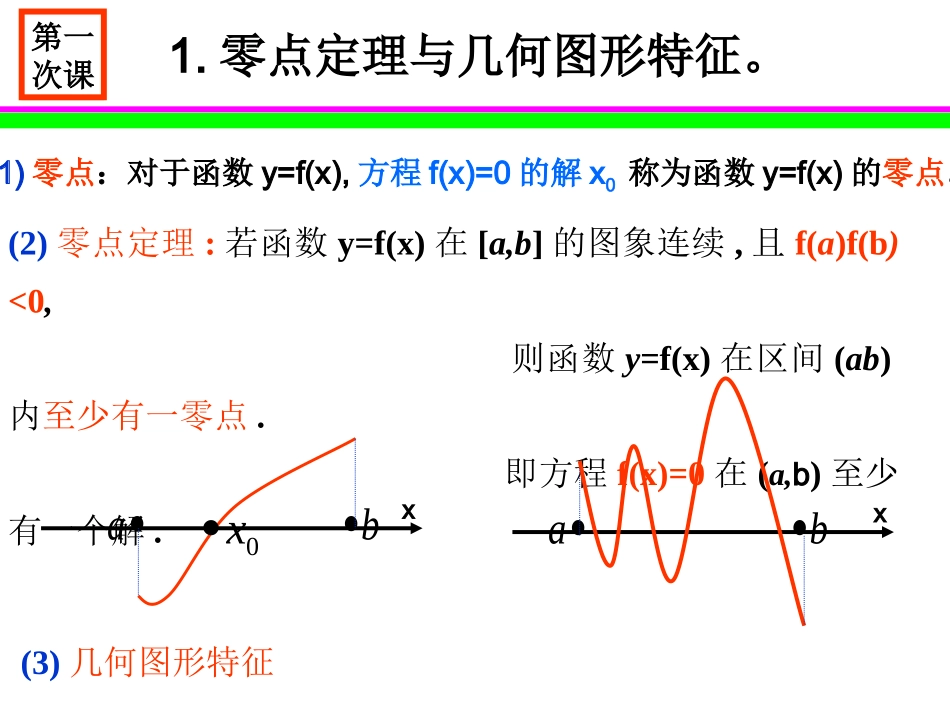
第12讲零点定理与根的分布知识要点1.零点定理与其几何特征。4.三次函数极值与其二次导函数根的关系。2.二次函数根的分布条件。5.三次方程根的个数与分布。3.函数极值存在条件。1.零点定理与几何图形特征。(1)零点：对于函数y=f(x),方程f(x)=0的解x0称为函数y=f(x)的零点。(2)零点定理:若函数y=f(x)在[a,b]的图象连续,且f(a)f(b)<0,则函数y=f(x)在区间(ab)内至少有一零点.即方程f(x)=0在(a,b)至少有一个解.abx0xabx(3)几何图形特征第一次课2.二次函数根的分布条件。例1.若函数f(x)=ax2-x-1,有且仅有一个零点,求实数a值.例2.若函数f(x)=x2+(a-1)x+1在区间[0,2]上有零点,求实数a值.例3.若函数f(x)=2ax2+2x-3-a在区间[-1,1]上有零点,求实数a值.2007年广东高考数学压轴题一级分类二级分类三级分类函数类型开口方向根的个数分类标准一次a=0二次a≠0向上a>0向下a<0一个零点两个零点{{{一个零点两个零点理清思路分级分类讨论综合扣题作答例3.若函数f(x)=2ax2+2x-3-a在区间[-1,1]上有零点,求实数a值.解.若a=0,f(x)=2x-3=0的解,x=1.5不在区间[-1,1].若a>0,y=f(x)的对称轴x=-1/(2a)<0当f(x)的对称轴在区间[-1,1]之左时.111022(1)(1)0(5)(1)0{{aaffaaa当f(x)在对称轴在区间[-1,1]之间时.110248(3)0[1,)(1)10aaaafa若a<0,y=f(x)的对称轴x=-1/(2a)>0当f(x)对称轴在区间[-1,1]之右时.111022(1)(1)0(5)(1)0{{aaffaaa当f(x)对称轴在区间[-1,1]之间)时.110223748(3)0(,]2(1)50aaaafa37(,][1,)2a综上所述:说明:根的分布问题必须数形结合3.函数极值点的存在条件。例5.(2007年山东文)若函数f(x)=ax2+blnx,ab≠0:证明:当ab>0时f(x)没有极值点;当ab<0时,f(x)有且只有一个极值点,并求出极值.极点存在条件:(1)函数y=f(x)在区间[m,n]上有定义;(2)若函数y`=f`(x)在[m,n]的图象连续;(3)f`(m)f`(n)<0.则:函数y=f(x)在区间(m,n)内至少有一极点,即方程f`(x)=0在(m,n)至少有一个解.第二次课3.函数极值点的存在条件。问题:三次函数是否一定有极值点?例4.若函数f(x)=x3+ax+a2-6有三个单调区间,求实数a取值范围.三次函数f(x)有极值方程f`(x)=0有不等实根△>04.三次方程解的个数问题。例6.若函数f(x)=ax3-1.5(a+2)x+6试讨论曲线y=f(x)与x轴的公共点的个数.例7.(2007全国理二)若函数f(x)=x3-x,(1)求曲线y=f(x)在点M(t,f(t))处的切线方程;(2)设a>0,如果过点(a,b)可作曲线y=f(x)的三条切线求证:-a