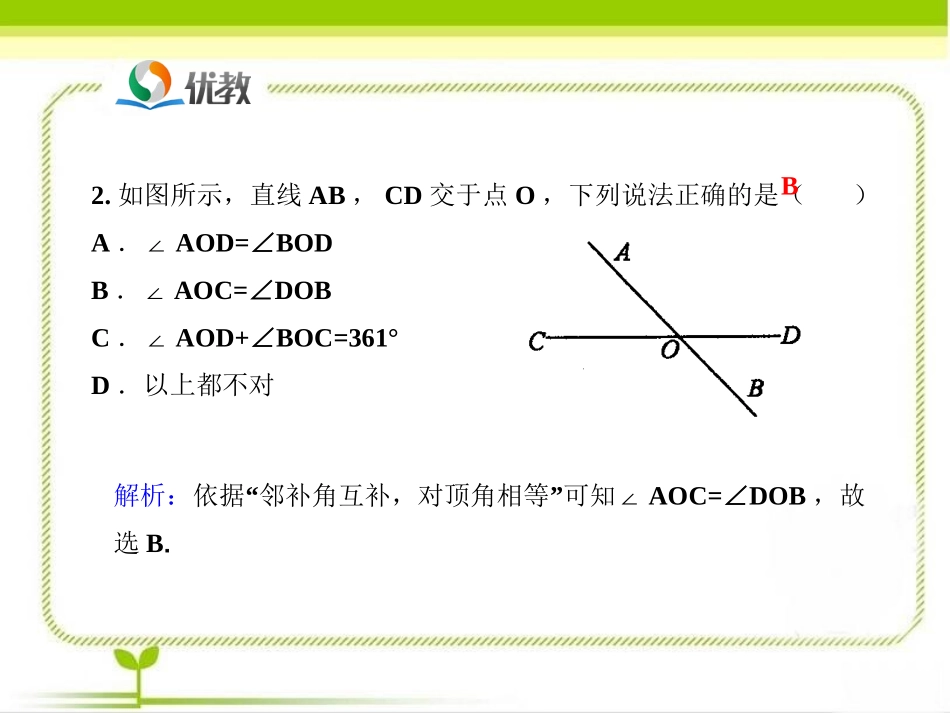
《相交线》即时练习1.填空:如图所示,取两根木条a,b,将它们钉在一起,就得到一个相交线的模型,其中∠1和∠2是_______,且∠1+2=_______∠,同理∠2与∠4,∠3与________,∠1与∠3都是邻补角.邻补角180°∠42.如图所示,直线AB,CD交于点O,下列说法正确的是()A.∠AOD=∠BODB.∠AOC=∠DOBC.∠AOD+∠BOC=361°D.以上都不对解析:“”依据邻补角互补,对顶角相等可知∠AOC=∠DOB,故选B.B3.下列四个图中,∠1和∠2是对顶角的图的个数是()A.0个B.1个C.2个D.3个解析:两个角是对顶角应同时满足的条件:①两个角有一个公共的顶点,②一个角的两边分别是另一个角的两边的反向延长线,故看图可知图①②④均不满足条件二,图③条件一、二均不满足,故选A.A4.如下图,直线AD、BC相交于点O,则关于∠AOC的对顶角和邻补角叙述正确的是()A.∠AOC各有1个对顶角和邻补角B.∠AOC有2个对顶角,1个邻补角C.∠AOC的对顶角是∠BOD,邻补角是∠COD和∠AOBD.∠AOC的对顶角是∠COD,邻补角是∠BOD和∠AOBC解析:根据邻补角及对顶角的定义可知∠BOD是∠AOC的对顶角,∠COD和∠AOB均是∠AOC的邻补角,故选C.OABCD5.下列说法正确的有()①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.A.1个B.2个C.3个D.4个解析:依据对顶角的性质可得:对顶角一定相等,但相等的角不一定是对顶角.因此分析①②③④可得仅①③正确,故选B.B6.如图所示,直线L1,L2,L3相交于一点,则下列答案中,全对的一组是()A.∠1=90°,∠2=30°,∠3=4=60°∠B.∠1=3=90°∠,∠2=4=30°∠C.∠1=3=90°∠,∠2=4=60°∠D.∠1=3=90°∠,∠2=60°,∠4=30°解析:根据对顶角相等的性质可得:∠2=60°,∠4=30°,∠1=∠3,又因为邻补角互补得出∠1=90°,故选D.D7.如图,直线AB、CD、EF相交于点O,∠AOE=40°,∠BOC=AOC∠,求∠DOF.解:设∠AOC=x°,则∠BOC=(2x)°.因为∠AOC与∠BOC是邻补角,所以∠AOC+BOC=180°∠所以x+2x=180解得x=60所以∠AOC=60°.因为∠DOF与∠EOC是对顶角,所以∠DOF=EOC=AOC-AOE=60°∠∠∠-40°=20°.8.如图,两条笔直的街道AB、CD相交于点O,街道OE、OF分别平分∠AOC、∠BOD,说明街道EOF是笔直的.解:因为∠AOC与∠BOD是对顶角,所以∠AOC=BOD.∠因为∠1=AOC∠,∠2=BOD∠,所以∠1=2.∠因为AB为直线,∠2与∠AOF是邻补角.所以∠2+AOF=180°.∠所以∠1+AOF=180°.∠即∠EOF=180°.所以EOF是一条直线,即街道EOF是笔直的.9.如图,已知∠2与∠BOD是邻补角,OE平分∠BOD,OF平分∠COE,∠2:1=4:1∠,求AOF.解:设∠1=x,则∠2=4x因为OE平分∠BOD,所以∠BOD=21=2x∠因为∠2+BOD=180°∠,所以4x+2x=180°,解得x=30°.因为∠DOE+COE=180°∠,所以∠COE=150°.因为OF分∠COE,所以∠COF=COE=75°.∠因为∠AOC与∠BOD是对顶角,所以∠AOC=BOD=60°.∠所以∠AOF=AOC+COF=60°+75°=135°.∠∠结束