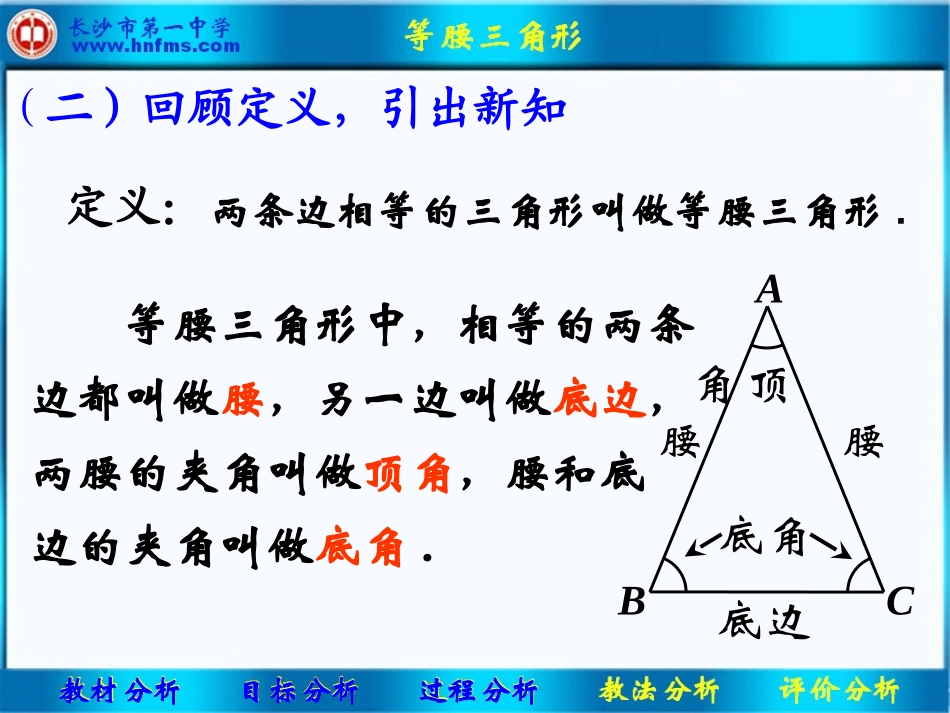
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?教材分析目标分析过程分析(一)创设情景,激发兴趣(二)回顾定义,引出新知定义:两条边相等的三角形叫做等腰三角形.等腰三角形中,相等的两条边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.教材分析目标分析过程分析ABC底边腰腰顶角底角⑴由“两边相等”得到“等腰三角形”. △ABC中,AB=AC,∴△ABC是等腰三角形.⑵由“等腰三角形”得到“两边相等”.如图, △ABC是等腰三角形∴AB=AC.教材分析目标分析过程分析(二)回顾定义,引出新知定义的理解:设计意图1.培养学生正向思维和逆向思维的能力;2.培养学生文字语言、图形语言和符号语言的转化能力.ABC(三)实践探索,感受特征请拿出准备的三边不等的三角形纸片,试一试,通过折叠一次,剪一次,是否可以剪出一个等腰三角形呢?(小组合作,看有何发现?)观察你所得到等腰三角形,你发现等腰三角形具有哪些特征?教材分析目标分析过程分析和底边上的高,(三)实践探索,感受特征教材分析目标分析过程分析等腰三角形1.是一个轴对称图形;2.两个底角相等,简称“等边对等角”.3.AD垂直于BC底边上的中线、互相重合,简称“三线合一”.AD平分∠BACAD平分BC顶角平分线、∠B=∠C练习:判断正误(口答)(1)如图,在△ABC中,∴∠B=∠C. AB=BC,CAB教材分析目标分析过程分析设计意图提醒学生注意使用“等边对等角”时,边与角的对应关系.练习:判断正误(口答)教材分析目标分析过程分析设计意图提醒学生注意“等边对等角”只能在同一个三角形中使用.(2)如图,在△ABC中, AC=BC,∴∠ADC=∠BEC.CABDE例:已知,在△ABC中,AB=AC,∠B=80,º求∠C和∠A的度数.∠A=80º,求∠C和∠B的度数.变式1.已知,在△ABC中,AB=AC,变式2.已知,在△ABC中,AB=AC,底角比顶角大15º,求∠A、∠B和∠C的度数.教材分析目标分析过程分析设计意图在等腰三角形中,①已知一个角,如何求另两个角的方法;②锐角可做底角、也可做顶角,但直角或钝角只能做顶角.引导学生利用代数的方法解决几何问题,强化方程的思想.ABC(三)实践探索,感受特征教材分析目标分析过程分析等腰三角形1.是一个轴对称图形;2.两个底角相等,简称“等边对等角”.3.顶角平分线、底边上的中线、和底边上的高,互相重合,简称“三线合一”.建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?教材分析目标分析过程分析变式3.已知,如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=80º,求∠1和∠ADC的度数.解:因为等腰三角形的“三线合一”,所以AD是△ABC的角平分线、底边上的高,即∠1=∠2,∠ADC=90.º因为∠BAC=180-º80-º80º=20º,所以∠1=10.º教材分析目标分析过程分析设计意图让学生进一步体会“三线合一”中“三线”之间互为因果的关系.ABCD12例.已知,在△ABC中,AB=AC,∠B=80º,求∠C和∠A的度数.变式3.已知,在△ABC中,AB=AC,D是BC边上的中点,∠B=80º,求∠1和∠ADC的度数.变式1.已知,在△ABC中,AB=AC,∠A=80º,求∠C和∠B的度数.变式2.已知,在△ABC中,AB=AC,底角比顶角大15º,求∠A、∠B和∠C的度数.(四)发散练习,拓展提高教材分析目标分析过程分析ABC教材分析目标分析过程分析(四)发散练习,拓展提高“”这个前提下,添加适当的条件,你还能得出什么结论?请说明理由.在△ABC中,AB=AC教材分析目标分析过程分析设计意图(四)发散练习,拓展提高引出等边三角形的定义、等边三角形与等腰三角形的关系、等边三角形的特征,完成腰和底边不等的等腰三角形与等边三角形相关知识的类比表格.图形等腰三角形(腰与底边不等)等边三角形定义两边相等的三角形三边都相等的三角形特征关系等边三角形一定是等腰三角形,等腰三角形不一定是等边三角形.轴对称图形(3条)等边对等角三线合一各内角都是60º轴对称图形(1条)等...