平面向量的基本定理VIP免费

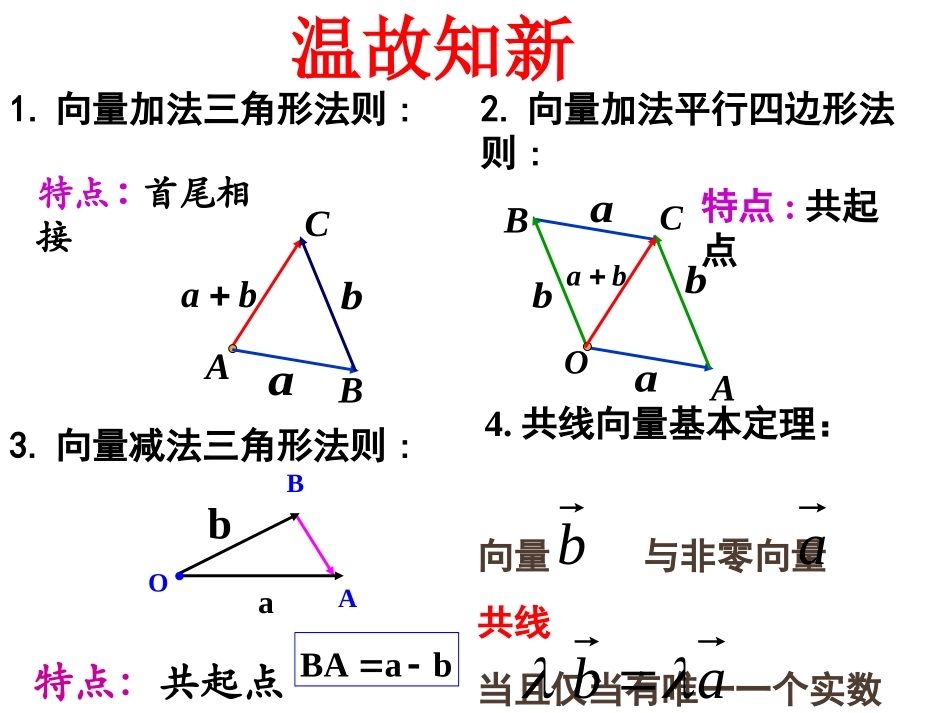
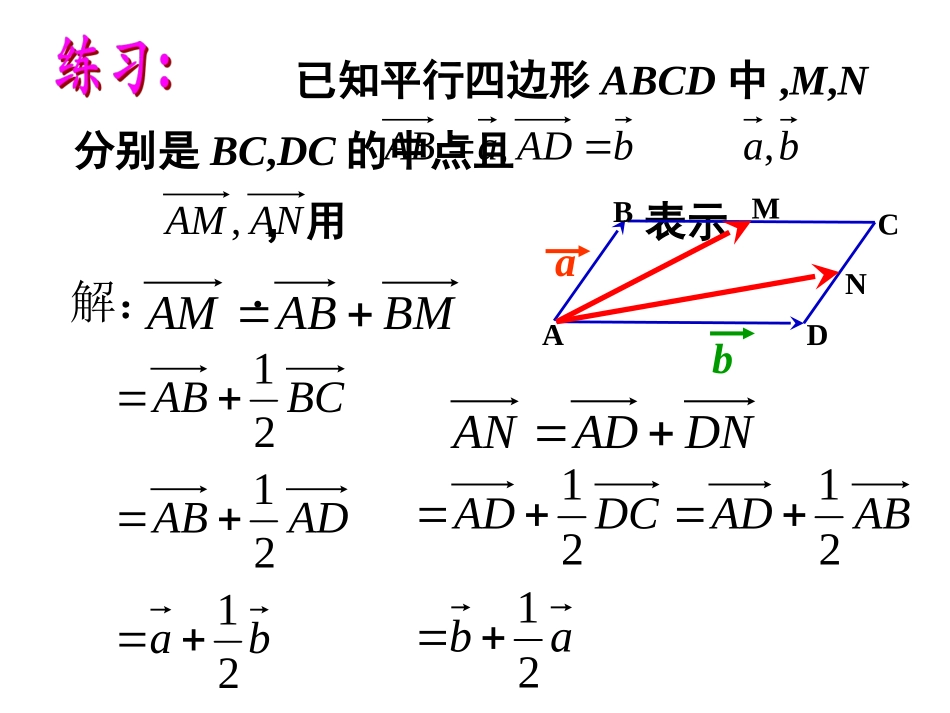
aAbBCbaaaAbBbOCba特点:首尾相接特点:共起点bBaABAab�2.向量加法平行四边形法则:O特点：共起点1.向量加法三角形法则:3.向量减法三角形法则:4.共线向量基本定理：向量与非零向量共线当且仅当有唯一一个实数，使得abab温故知新已知平行四边形ABCD中,M,N分别是BC,DC的中点且，用表示.bADaAB,ba,ANAM,ADBCMNbaBMABAM解：DNADANbaADABBCAB212121abABADDCAD212121问题:一天,2只住在正西方向的大猴子和4只住在北偏东30°方向的小猴子同时发现一筐桃子,他们分别朝着自己住的方向拉,已知每只大猴子的拉力是100牛顿,每只小猴子的拉力是50牛顿,问这筐桃子往哪边运动?问题:一天,2只住在正西方向的大猴子和4只住在北偏东30°方向的小猴子同时发现一筐桃子,他们分别朝着自己住的方向拉,已知每只大猴子的拉力是100牛顿,每只小猴子的拉力是50牛顿,问这筐桃子往哪边运动?如果是1只大猴子和4只小猴子呢?NMe1e2a如果要让这筐桃子往我们指定的方向运动,如何改变大小猴子的数量?aCe1e2oBAOC=OM+ON=xe1+ye21e�2e�OCABMNa11eOM22eON设是同一平面内的两个不共线的向量，是这一平面内的任一向量，问：与之间有怎样的关系？21,eea21,eea2211eeONOMa？来表示呢任意一个向量都可以用后，是否平面内，确定一对不共线向量221121eeee想一想⑴a1e2ea1e2e.02121即可使结论成立为或共线时，可令或与当eea⑵？怎样构造平行四边形况时，的位置如下图两种情改变aa1e2ea1e2eO2eAOCB'BNMCAB'A1eNM⑵？怎样构造平行四边形况时，的位置如下图两种情改变a1e2eaAOB'B'ANM1e2eaAOBCNM'Ca2e1e一、平面向量基本定理:如果是同一平面内的两个不共线向量，那么对于这一平面内的任一向量有且只有一对实数,使21ee、a21、2211eea.21所有向量的一组基底叫做表示这一平面内，其中ee2、基底不唯一，关键是不共线.4、基底给定时，分解形式唯一.说明：1、把不共线的非零向量叫做表示这一平面内所有向量的一组基底.12,ee�3、由定理可将任一向量在给出基底的条件下进行分解.12,ee�a动画1.练习2.3.设是两个不共线向量，已知若A,B,D三点共线，求实数？,2bkaABkba,,3baCB,2baCDbDC21解：DCADBABCbab21ba21ANDAMDMNbab21)21(21ab411.//2,,,,ABCDABCDABCDMNDCBAADaABbabDCBCMN���例如图梯形中，，，、是，中点，，试以为基底表示aABDCNMb二、向量的夹角:OABba两个非零向量和,作，,则)1800(abAOB叫做向量和的夹角．OAa�OBb�ab夹角的范围：00180,0180与反向abOABab0与同向abOABab记作ab90与垂直，abOABab注意:两向量必须是同起点的例2:如图，等边三角形中，求(1)AB与AC的夹角；(2)AB与BC的夹角。ABC60'C0120ABCDoxyija如图，是分别与x轴、y轴方向相同的单位向量，若以为基底，则,ij,ij+aaijxyxy对于该平面内的任一向量，有且只有一对实数、，可使这里，我们把（x,y）叫做向量的（直角）坐标，记作a(,)axy①其中，x叫做在x轴上的坐标，y叫做在y轴上的坐标，①式叫做向量的坐标表示。aa三、平面向量的坐标表示OxyAijaxy+axiyj+OAxiyj�当向量的起点在坐标原点时，向量的坐标就是向量终点的坐标.坐标(x,y)一一对应两个向量相等，利用坐标如何表示？2121yyxxba且向量a三、平面向量的坐标表示例4:已知，求的坐标.1122(,),(,)AxyBxyAB�xyOBAABOBOA�2211(,)(,)xyxy2121(,)xxyy一个向量的坐标等于表示此向量的有向线段的终点的坐标减去起点的坐标.解：.,并求出它们的坐标、、、分别表示向量，如图，用基底dcbaji.5例jiAAAAa3221解：(2,3)a)3,2(32jib)3,2(32jic)3,2(32jidjyxOiaA1AA2bcdB)3,2()2,2()5,4(ABa.1,nmOBnOAmOPABPBAO且则上，在直线若点三点不共线，、、已知本题的实质是：OABP.,),R(,,OPOBOAtABtAPOBOA表示用且不共线、如图.3例一个重要结论OBtOAtOP)1(小结1.平面向量基本定理:2.向量的夹角:3.平面向量的坐标表示4.一个重要结论