平面向量数量积的坐标表示模夹角VIP免费

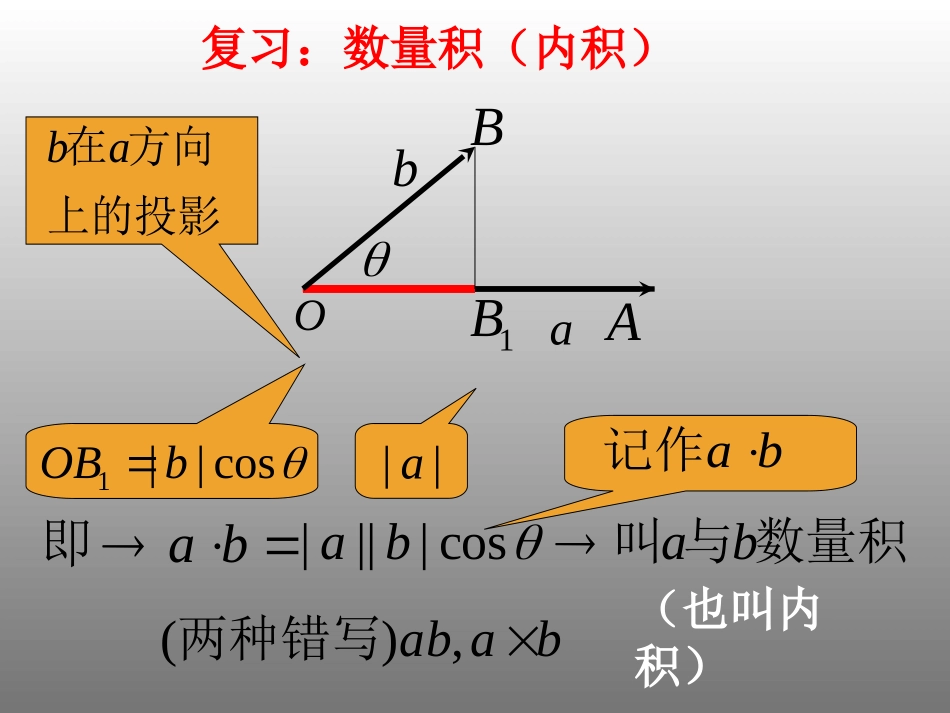
2.4.2平面向量数量积的坐标表示、模、夹角复习：数量积（内积）aOAbB1B1||cosOBbba在方向上的投影||||cosabab叫与数量积ab即ab记作（也叫内积）(),abab两种错写||aixjyobiijjij111122(,),(,)axybxy设:一、平面向量数量积的坐标表示:01122,axiyjbxiyj则:a一.平面向量数量积的坐标表示:（合作探究）1122,,,0,0axybxyab1212abxxyy22bxiyj2212122112xxixyijxyijyyj221,0,1iijj11,axiyj)()(2211jyixjyixba两个向量的数量积等于它们对应坐标的乘积的和.二、向量的模和两点间距离公式:1()(,),axy向量的模长度公式：设2121,ABxxyy�则222,aaaxy则222121ABxxyy�11222,,,AxyBxy设、22axy或三、向量垂直和平行的坐标表示（自主探究）(1)垂直:(2)平行:0abab//abba1122,,,(0,0)axybxyab12120xxyy1221xyxy四、向量夹角公式的坐标表示:0,,,,2211，夹角为与设bayxbyxacos||||abab1212xxyy2211xy2222.xy1:1(3,1),(1,2),||||.abababab例已知求，，与的夹角||||ab412125abxxyy解2211xy2222.xy52cos||||abab52522五.应用举例22,3,2,4,.ababab已知则(0,7),(4,1)abab法一：22ababab法二：（）（）047(1)7.abab（）（）22||||13207ab例2.已知A(1,2)，B(2,3)，C(2,5)，求证：△ABC是直角三角形证明：即AB⊥AC，△ABC是直角三角形.330ABAC�1,1AB3,3AC2,4BC想一想：还有其他解法吗？52,23,2BCACAB六.巩固练习：第107页1，2，3题12121.abxxyy2221212.ABxxyy�12123.0abxxyy12214.//abxyxy1212222211225.cos.xxyyxyxy七.课堂小结八.作业布置:（下一节课上习题课）1.教材第108页A组第5，8，9，10，11题2.教材第108页B组第2，4题解:设所求向量为(x,y),则103422yxyx54535453yxyx或)54,53()54,53(bb或(4,3),aab例3:已知求与垂直的单位向量【习题课】例4:已知=(1,0)，=(2,1)，当k为何实数时，向量k－与+3(1)平行；(2)垂直所以k=13(2)由向量垂直条件得7(k－2)－3=0所以k=177ababab(1)由向量平行条件得3(k－2)=-7解：k－=(k－2,－1)ab+3=(7,3)abB练习CD3231m=-26A12121.abxxyy2221212.ABxxyy�12123.0abxxyy12214.//abxyxy1212222211225.cos.xxyyxyxy小结作业:下一节课上习题课1.教材第108页A组第5，8，9，10，11题2.教材第108页B组第2，4题