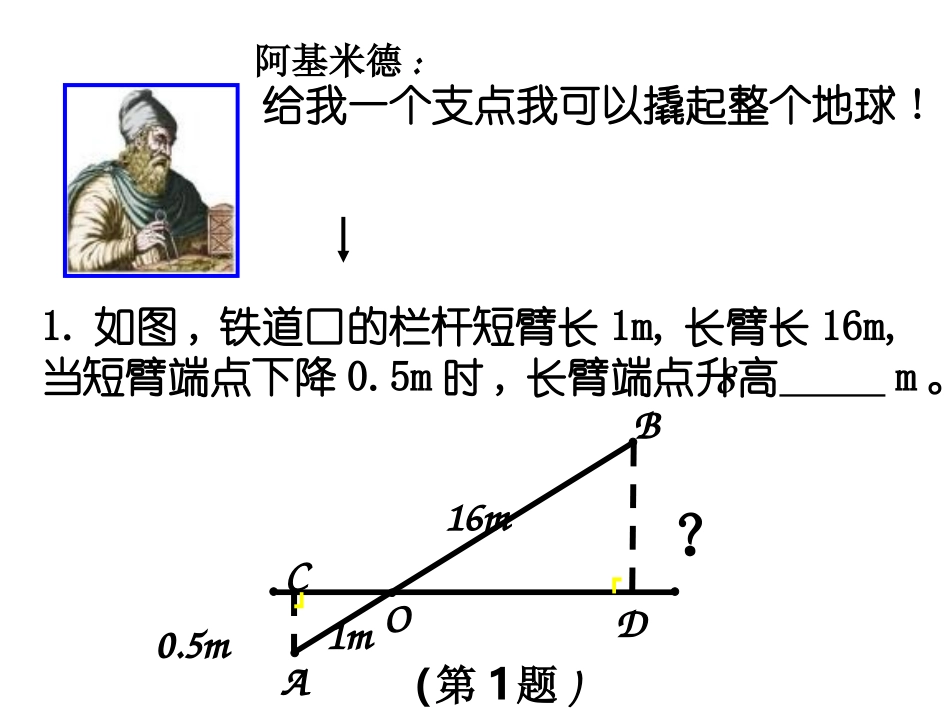
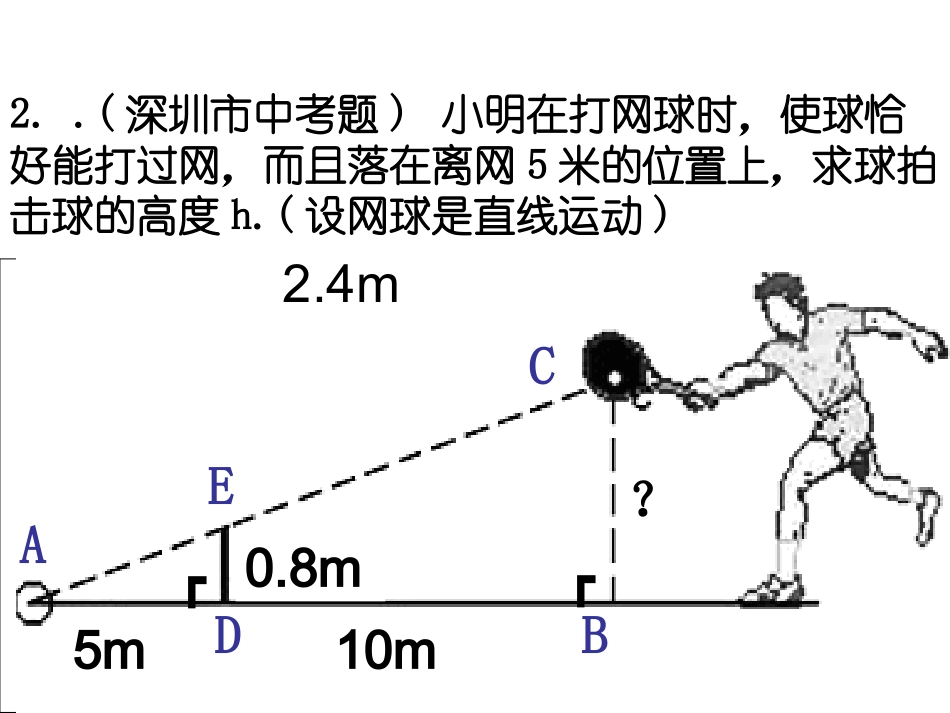
1、相似三角形的判别方法有哪些?2、相似三角形的性质有哪些?复习复习1.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高m。OBDCA┏┛(第1题)8给我一个支点我可以撬起整个地球!阿基米德:1m16m0.5m?2..(深圳市中考题)小明在打网球时,使球恰好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.(设网球是直线运动)ADBCE┏┏0.8m5m10m?2.4m胡夫金字塔是埃及现存规模最大的金字塔,被喻为“世界古代七大奇观之一”。塔的4个斜面正对东南西北四个方向,塔基呈正方形,每边长约230多米。1.测量金字塔高度据说,埃及的大金字塔修成一千多年后,还没有人能够准确的测出它的高度。有不少人作过很多努力,但都没有成功。一年春天,泰勒斯来到埃及,人们想试探一下他的能力,就问他是否能解决这个难题。泰勒斯很有把握的说可以。第二天,法老如约而至,金字塔周围也聚集了不少围观的老百姓。泰勒斯来到金字塔前,根据自己的测量,得出了金字塔确切的高度。在法老的请求下,他向大家讲解了其中的原理,也就是今天所说的相似三角形定理。同学们是不是也想试试呢?如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与线段长AB,能否近似算出金字塔的高度OB?A’B’O’ABO如何测量AB的长度?A’B’O’ABO答:即该金字塔高为137米.解:由于太阳光是平行光线,因此∠OAB=∠O′A′B′.13721274BABOAB(米)OB=又因为∠ABO=∠A′B′O′=90°.所以△OAB∽△O′A′B′,OB∶O′B′=AB∶A′B′,如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB.ACBDE┐┐请列出比例式DE:BC=AE:AC还可以这样测:还可以这样测:ACBDE┐┐还可以这样测:还可以这样测:若BC=1.6mAC=3mCE=15m求DE的长测高的方法测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决:物高1:物高2=影长1:影长2也可以理解为:测量不能到达两点间的距离,常构造相似三角形,利用相似三角形的性质解决求出线段的长。2.测量树高小明﹑小李﹑小王三位同学想利用树影测量树高.(1)小明测得长为1米的竹竿影长为0.9米,同时,小李测得一棵树的影长为5.4米,请计算小明测量这棵树的高.由相似三角形性质得:树高竿高树影长竿影长5.40.91(1)小明测得长为1米的竹竿影长为0.9米,同时,小李测得一棵树的影长为5.4米,请计算小明测量这棵树的高;(2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2mBACD2.测量树高(1)小明测得长为1米的竹竿影长为0.9米,同时,小李测得一棵树的影长为5.4米,请计算小明测量这棵树的高;(2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2mBAC解:画CG⊥AB于G,CG=BD=2.7,BD=CD=1.2答:这棵树的高为4.2米.DG由相似三角形的性质得:AG:CG=1:0.9∴AG=2.7÷0.9=3AB=AG+BG=4.22.测量树高方法一由相似三角形的性质得:BE12.70.9(1)小明测得长为1米的竹竿影长为0.9米,同时,小李测得一棵树的影长为5.4米,请计算小明测量这棵树的高;(2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2m解:如图,过点D画DEAC∥交AB于E点,由平行四边形ACDE得AE=CD=1.2,BADCE∴BE=3,AB=BE+AE=4.2答:这棵树高有4.2米.2.测量树高方法二(1)小明测得长为1米的竹竿影长为0.9米,同时,小李测得一棵树的影长为5.4米,请计算小明测量这棵树的高;(2)同时小王在测另一棵树时,发现树影的一部分在地面上,而另一部分在墙上,他测得地面上的影长为2.7米,留在墙上部分的影长为1.2米.请计算小王测量的这棵树的高.2.7m1.2mBAC解:延长AC交BD延长线于G,由相似三角形的性质得:CD:DG=1:0.9DG=0.9CD=1.08∴BG=BD+DG=3.78由CD:AB=DG:BG得AB=4.2答:这棵树的高为4.2米.DG2.测量...