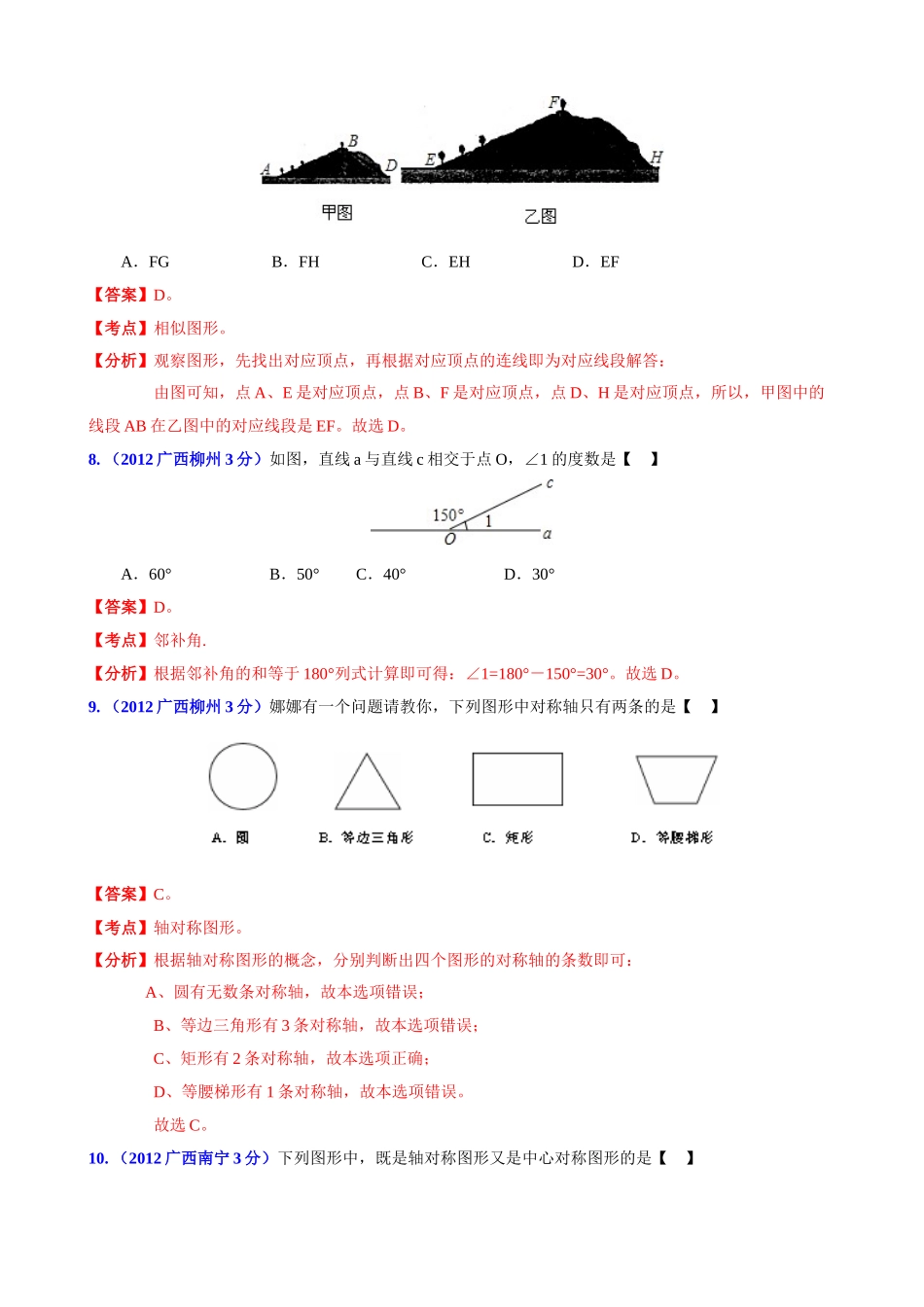
广西各市2012年中考数学试题分类解析汇编专题8:平面几何基础一、选择题3.(2012广西桂林3分)如图,与∠1是内错角的是【】A.∠2B.∠3C.∠4D.∠5【答案】B。【考点】“三线八角”问题。【分析】根据内错角的定义,两直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角是内错角。因此,∠1的内错角是∠3。故选B。4.(2012广西桂林3分)下面四个标志图是中心对称图形的是【】【答案】B。【考点】中心对称对形。【分析】根据中心对称图形的概念,中心对称图形是图形沿对称中心旋转180度后与原图重合。因此,根据各图特点,只有选项B符合。故选B。5.(2012广西河池3分)如图,把一块含有角的直角三角板的两个顶点分别放在直尺的一组对边上.如果,那么的度数是【】[来源:学#A.B.C.D.【答案】【考点】平行线的性质。【分析】根据直角三角板的性质得出∠AFE的度数,再根据平行线的性质求出∠2的度数即可:如图, △GEF是含45°角的直角三角板,∴∠GFE=45°。 ∠1=25°,∴∠AFE=∠GEF-∠1=45°-25°=20°。 AB∥CD,∴∠2=∠AFE=20°。故选C。6.(2012广西来宾3分)在下列平面图形中,是中心对称图形的是【】A.B.C.D.【答案】B。【考点】中心称对形。【分析】根据中心对称图形的概念,中心对称图形是图形沿对称中心旋转180度后与原图重合。因此,只有选项B符合,故选B。7.(2012广西柳州3分)小张用手机拍摄得到甲图,经放大后得到乙图,甲图中的线段AB在乙图中的对应线段是【】ABCDA.FGB.FHC.EHD.EF【答案】D。【考点】相似图形。【分析】观察图形,先找出对应顶点,再根据对应顶点的连线即为对应线段解答:由图可知,点A、E是对应顶点,点B、F是对应顶点,点D、H是对应顶点,所以,甲图中的线段AB在乙图中的对应线段是EF。故选D。8.(2012广西柳州3分)如图,直线a与直线c相交于点O,∠1的度数是【】A.60°B.50°C.40°D.30°【答案】D。【考点】邻补角.【分析】根据邻补角的和等于180°列式计算即可得:∠1=180°-150°=30°。故选D。9.(2012广西柳州3分)娜娜有一个问题请教你,下列图形中对称轴只有两条的是【】【答案】C。【考点】轴对称图形。【分析】根据轴对称图形的概念,分别判断出四个图形的对称轴的条数即可:A、圆有无数条对称轴,故本选项错误;B、等边三角形有3条对称轴,故本选项错误;C、矩形有2条对称轴,故本选项正确;D、等腰梯形有1条对称轴,故本选项错误。故选C。10.(2012广西南宁3分)下列图形中,既是轴对称图形又是中心对称图形的是【】A.B.C.D.【答案】A。【考点】轴对称图形和中心称对形。【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。因此,同时满足两个条件的是A图形。故选A。11.(2012广西钦州3分)下列四幅图案中,既是轴对称图形又是中心对称图形的是【】A.B.C.D.【答案】D。【考点】轴对称图形和中心对称图形。【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。因此,A、不是轴对称图形,也不是中心对称图形,不符合题意;B、是轴对称图形,不是中心对称图形,不符合题意;C、不是中心对称图形,是轴对称图形,不符合题意;D、是轴对称图形,也不是中心对称图形,符合题意。故选D。12.(2012广西钦州3分)下列说法错误的是【】A.两点之间线段最短B.对顶角相等C.为了了解生产的一批炮弹的杀伤半径,适宜采用全面调查的方式D.“通常加热到100℃时,水沸腾”这个事情属于必然事件【答案】C。【考点】线段的性质,对顶角的性质,全面调查与抽样调查,必然事件。【分析】根据线段的公理,对顶角的性质,抽样调查的事件的特点,必然事件的定义求解:A、两点之间线段最短,正确,故选项错误;B、对顶角相等,正确,故选项错误;C、了解生产的一批炮弹的杀伤半径,调查过程带有破坏性,只能采取抽样调查,而不能将整批炮弹全部用于实验,错误,故选项正确;D、“通常加热到100...