平面向量基本定理VIP免费

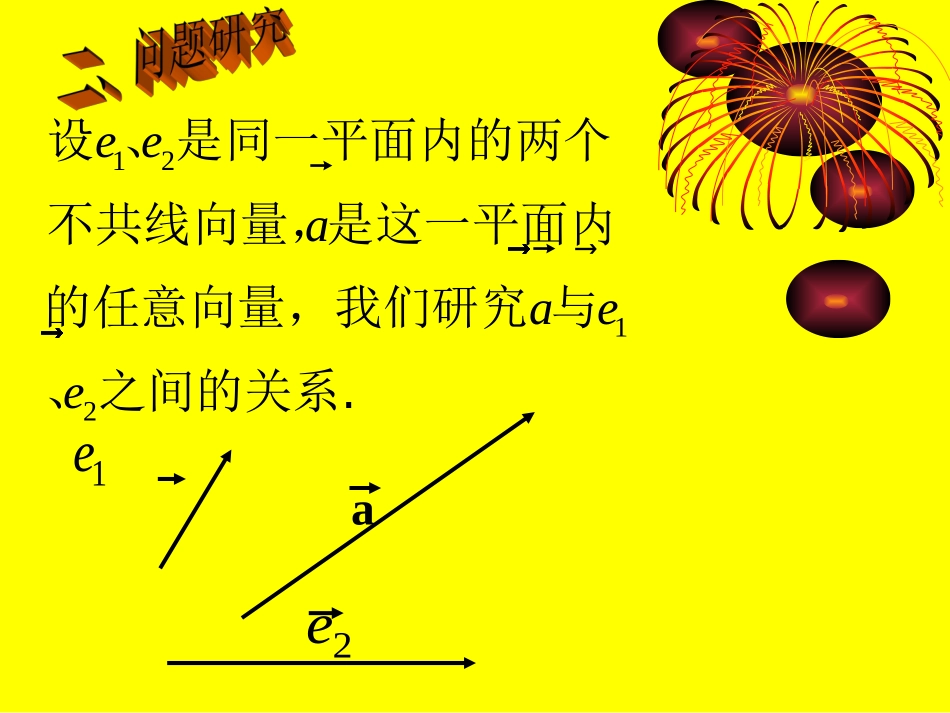
2.3.12.3.1平面向量基本定理平面向量基本定理1、向量加法的平行四边形法则2、共线向量的基本定理1ea2e1212eeaaee����设、是同一平面内的两个不共线向量，是这一平面内的任意向量，我们研究与、之间的关系.OC=OM+ON=21OA+OB11e2e2即a=+.1ea1eA2eOaCB2eNMMN一向量a有且只有一对实数、使21共线向量，那么对于这一平面内的任如果、是同一平面内的两个不1e2e11ea=+2e2这一平面内所有向量的一组基底。我们把不共线的向量、叫做表示1e2e（1）一组平面向量的基底有多少对？（有无数对）（基底不唯一，关键是不共线）思考1EFANBaMOCNMMOCNaE思考2(2)若基底给定，则分解形式唯一。特别的，若a=0，则有且只有：可使0=11e2e2+.21==0？若与中只有一个为零，情况会是怎样？21特别的，若a与（）共线，则有=0（=0），使得:a=+.121e22e2e11e向量的夹角:a,bOAOB�=a,=b已知两个非零向量，作，则00(0180)AOB叫做向量ab与的夹角.OBAab当00时，a与b同向；当0180时，a与b反向；当090时，a与b垂直，记作ab.1e2e15.2e23eOABC·12122.53.eeee�例1、已知向量、，求作1eOAC·M.ABCDABaADbabMAMBMCMD����例2、如图所示，平行四边形的两条对角线相交于点，且，，用、表示、、、DCBAM例3、如图，已知梯形ABCD，AB//CD，且AB=2DC,M,N分别是DC,AB的中点.请大家动手,在图中确定一组基底，将其他向量用这组基底表示出来。ANMCDB解析：BC=BD+DC=MN=DN-DM21=(AN-AD)-DC(AD–AB)+DCANMCDBDC=AB=21211e设AB=,AD=,则有：1e2e41=-.2e1e1e2e1e21=-+=2141=--2e1e1e2e211e-+能够在具体问题中适当地选取基底，使其他向量能够用基底来表示，再利用有关知识解决问题。例4.在平行四边形ABCD中，E、F分别是DC和AB的中点，试判断AE,CF是否平行？FBADCEFBADCEE、F分别是DC和AB的中点,AE=AD+DE=b+a2121CF=CB+BF=-b-aAE=-CFAE与CF共线，又无公共点AE,CF平行.解：设AB=a,AD=b.5232.abABakbCBabCDabABDk�例、已知、是两不共线向量，且，，，若、、三点共线，求的值A、B、D三点共线解：AB与BD共线,则存在实数λ使得AB=λBD.λ使得AB=λBD.由于BD=CD–CB=(2a–b)–(a+3b)=a–4b从而2a+kb=(a–4b)于是由条件可得2=k=4k=8.本题在解决过程中用到了两向量共线的充要条件这一定理，并借助平面向量的基本定理减少变量，除此之外，还用待定系数法列方程，通过消元解方程组。这些知识和考虑问题的方法都必须切实掌握好。从而2a+kb=(a–4b)2-=0k–4=0此处可另解：k=8.即（2-）a+(k-4)b=0课堂练习oABM12ab（）abMAOBABOAOB�已知点是三角形的边的中点，若＝，＝，则OM变式探究：oABM�（1）若P是AB靠近A的三等分点，则OPabMAOBABOAOB�已知点是三角形的边的中点，若＝，＝，则OM12ab（）Pt��（2）若AP=AB，则OP2ab3�1OP＋31tatb�OP（－）＋BBOOAAPPt��（2）若AP=AB，则OP分析：分析：OP=OA+APOP=OA+AP()(1)APtABOPOAAPOAtABOAtOBOAtOAtOB����解：结论若A、B是直线Ｌ上任意两点，Ｏ是Ｌ外一点。则对直线Ｌ上任一点Ｐ，存在实数ｔ，使关于基底｛，｝的分解式为=（1－t）＋t（*）并且满足（*）式的点一定在L上OP�OA�OB�OP�OA�OB�说明：1（）向量等式（*）叫做直线L的向量参数方程式.其中实数ｔ叫做参变数，简称参数.(2MOAOBOMAB��1（2）特殊：当ｔ＝时，点是中点，2则＝线段中点的向量表达式）PAOMBL1、平面向量基本定理内容2、对基本定理的理解３、平面向量基本定理的应用求作向量、解向量问题、解平面几何问题12(1)实数对、的存在性与唯一性(2)基底的不唯一性(3)定理的拓展性五、课时小结