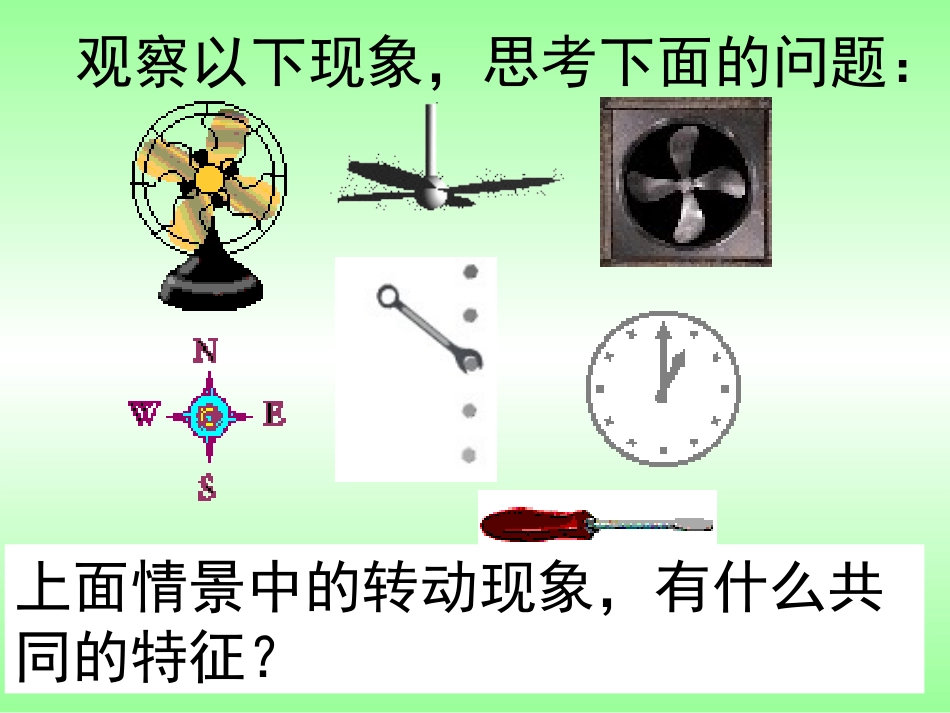
生活中的观察以下现象,思考下面的问题:上面情景中的转动现象,有什么共同的特征?这个定点称为旋转中心,转动的角称为旋转角。旋转角旋转中心在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为旋转。AoB如图,如果把钟表的指针看做四边AOBC,它绕O点旋转得到四边形DOEF.在这个旋转过程中:1)旋转中心是什么?2)经过旋转,点A、B分别移动到什么位置?3)旋转角是什么?4)AO与DO的长有什么关系?BO与EO呢?5)∠AOD与∠BOE有什么大小关系?旋转中心是O点D和点E的位置AO=DO,BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角(4)对应点到旋转中心的距离相等.旋转的基本性质(1)旋转不改变图形的大小和形状.(2)图形上的每一点都绕旋转中心沿相同方向转动了相同的角度(3)任意一对对应点与旋转中心的连线所成的角度都是旋转角.活动要求:1、画出基本图案三角形并标上字母2、绕三角形任意一个顶点沿任一方向(顺时针或逆时针)旋转一定角度,画出旋转后的图形,并标上字母。3、写出旋转中心、旋转方向、旋转角及其关系、对应点到旋转中心的距离及其关系。例1钟表的分针匀速旋转一周需要60分.(1)指出它的旋转中心;(2)经过20分,分针旋转了多少度?120动态演示解:(1)它的旋转中心是钟表的轴心;(2)分针匀速旋转一周需要60分,因此旋转20分,分针旋转的角度为1202060360做一做:在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.活动要求:1、把手中正方形纸板画在练习本上并标出字母。2、画出所画正方形的对角线并在交点处标出字母3、旋转正方形纸板,画出旋转后的正方形并标出字母。紫荆花做一做:在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.做一做:在图中,正方形ABCD与正方形EFGH边长相等,这个图案可以看作是哪个“基本图案”通过旋转得到的.练习:本图案可以看做是一个菱形通过几次旋转得到的?每次旋转了多少度?也可以看做是二个相邻菱形通过几次旋转得到的?每次旋转了多少度?还可以看做是几个菱形通过几次旋转得到的?每次旋转了多少度?3个1次18002次1200,24005次60012001800240030003个1次600生活中的数学补充练习:1、在平面内,将一个图形绕一个,沿某一个方向转动一个,这样的图形运动称为旋转.旋转不改变图形的和.2、钟表的时针旋转一周需12小时.(1)它的旋转中心是什么?(2)经过3小时,时针旋转了多少度?(3)经过几小时,时针旋转150度?