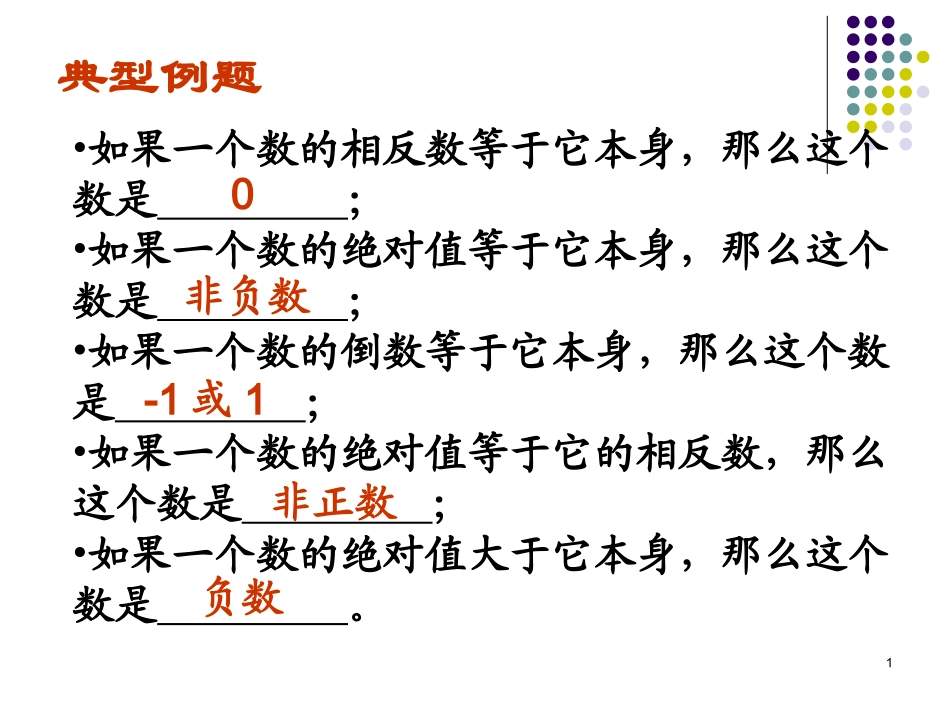
1典型例题•如果一个数的相反数等于它本身,那么这个数是;•如果一个数的绝对值等于它本身,那么这个数是;•如果一个数的倒数等于它本身,那么这个数是;•如果一个数的绝对值等于它的相反数,那么这个数是;•如果一个数的绝对值大于它本身,那么这个数是。0非负数-1或1非正数负数2科学记数法与近似数•科学记数法:用字母N表示数,则N=a×10n(1≤|a|<10,n是整数).•关键是让学生熟练掌握a和n的确定3典型例题用科学记数法记出下列各数:(1)月球的质量约是7340000000000000万吨;(2)银河系中的恒星数约是160000000000个;(3)地球绕太阳转的轨道半径约是149000000千米.)01.0(5972.1)2()(85149.0)1(精确到精确到千分位似值的要求对下列各数取近用四舍五入法按括号里)(60340)5(1018.44)(02076.0)3(3保留两个有效数字(精确到百位))(保留三个有效数字近似数与科学记数法相结合41.判断对错:(1)0是单项式,也是整式;(3)单项式的次数是7次;2325ab(2)是二次三项式;211xxx.)(5)(3)(2)4(222x-yx-yx-y典型例题2.当m等于什么时,22212325313mxyxyyxyxy是关于x,y的二次多项式?5例若M,N都是4次多项式,则M+N为()A.4次多项式B.8次多项式C.次数不超过4次的整式D.次数不低于4次的整式C典型例题6典型例题22π)8(;221)7(.312)6(;2)5(;01)4(;73)3(;32)2(1553)1(.1rSxxxxxxnmx;元一次方程:判断下列各式哪些是一2.已知方程(|k|-1)x2+(k-1)x+3=0是关于x的一元一次方程,求k的值.3.已知方程(k-2)(k-3)xk+(k+2)x+1=0是关于x的一元一次方程(其中k>0),试求k的值.k=-1k=1或k=2或k=3(5),(7)改成k-37区分常见易错之处)()(,)(22222--2--2-2-434322636263236263263626326)()()(8区分常见易错之处151152131321515115213132157-12126-121-12116-7-12126-12112116-)(9例计算:16+(-25)+24+(-32).解:原式=(16+24)+[(-25)+(-32)]=40+(-57)=-17.把正数和负数分别结合在一起计算就比较简便.常用的一些运算的注意事项或简便方法例7+5+(-4)+6+4+3+(-3)+(-2)+8+1.解:原式=[(-4)+(4)]+[5+(-3)+(-2)]+(7+6+3+8+1)=0+0+25=25.把相加得零的数结合起来相加.计算比较简便.10解:原式作分数加法时,先把同分母的或相加得整数的结合起来相加.计算比较简便.)()()计算(例724-753-513538512-531)8(1538]724-753-[]513512-[538)()()(常用的一些运算的注意事项或简便方法)()计算(例6-7624-解:原式71471461766124617624)(先定符号,合理使用分配律11)201011()411(3112112)(例常用的一些运算的注意事项或简便方法解:原式2011-20102011200920104534232-通过算式的规律确定负因数的个数为1005个,为奇数,因此符号为负.12例用“<”,“>”填空(1)如果ab>0,a+b>0,那么a___0,b___0;(2)如果ab>0,a+b<0,那么a___0,b___0;(3)如果ab<0,a>b,那么a___0,b___0运算中更一般的问题(略高要求)两数的同正、同负、异号如何用两数之和、积去表示例比较大小(1)当b>0时,a,a-b,a+b哪个最大?哪个最小?(2)当b<0时,a,a-b,a+b哪个最大?哪个最小?会根据加数的正负判断和或差的大小关系13合并同类项是要熟练掌握的基本方法(2)当m取何值时,-3y3mx3与4x3y6是同类项?(1)k为何值时,3xky与-x2y是同类项?例题212ab2)ab1+=(2-32系数相加不变;)合并同类项:(bababa22221323原式14合并同类项是要熟练掌握的基本方法系数相反找出同类项例题;)合并同类项:(3222234babbaabbaa322223babbaabbaa解:333223322223)11()11()()(bababbaabababbabaa15去括号、添括号法则是导致错误的一个关键点例题先去括号,再合并同类项:);()()()1(zyxzyxzyx);2()2()2(2222babababa).23(2)2(3)3(2222xyyx注意括号前面的符号161,1),45(322222...