配方法-121090VIP免费

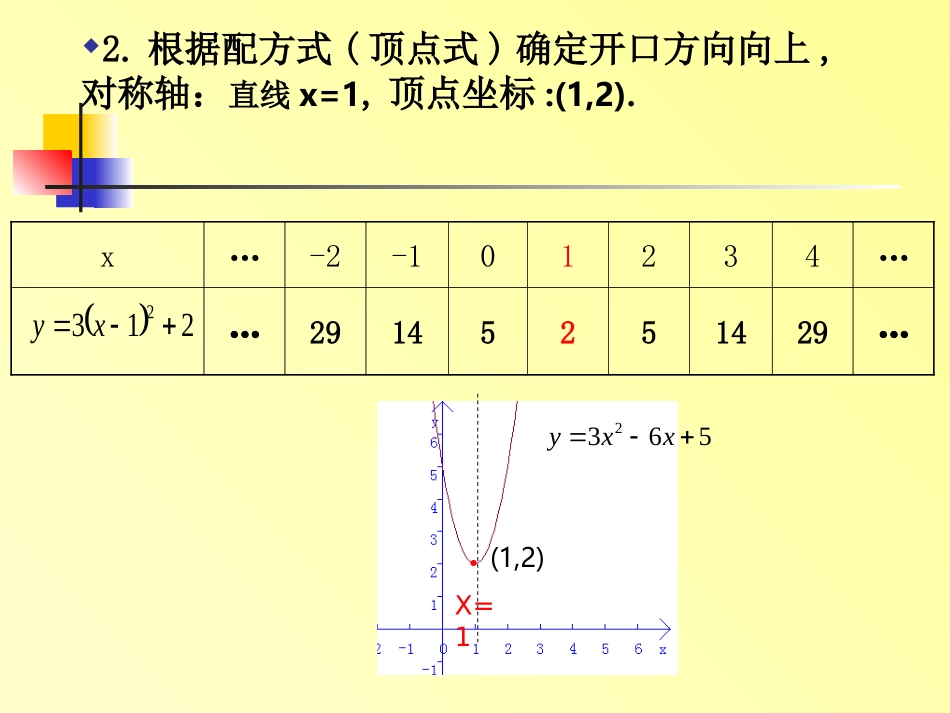
二次函数y=ax2+bx+c的图象和性质xy5632xxy35232xx提取二次项系数3511232xx配方:加上再减去一次项系数绝对值一半的平方32132x整理:前三项化为平方形式,后两项合并同类项.2132x化简:去掉中括号5632xxy我们知道，像y=a(x-h)2+k这样的函数，容易确定相应的顶点为（h,k）二次函数也能化成这样的形式吗？2.根据配方式(顶点式)确定开口方向向上,对称轴：直线x=1,顶点坐标:(1,2).x…-2-101234………2132xy…29145251429…X=1●(1,2)5632xxy一般地,对于二次函数y=ax+bx+c,²我们可以利用配方法推导出它的对称轴和顶点坐标.cbxaxy2acxabxa2提取二次项系数acababxabxa22222配方:加上再减去一次项系数绝对值一半的平方222442abacabxa整理:前三项化为平方形式,后两项合并同类项.44222abacabxa化简:去掉中括号?因此,二次函数y=ax²+bx+c的图象是一条抛物线.根据公式确定下列二次函数图象的对称轴和顶点坐标：.2:abx它的对称轴是直线.44,22abacab它的顶点是;13122.12xxy;319805.22xxy;2212.3xxy.2123.4xxy二次函数y=ax2+bx+c(a≠0)的图象和性质抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.根据图形填表：abacab44,22abacab44,22abx2直线abx2直线abacabx44,22最小值为时当abacabx44,22最大值为时当请你总结函数函数y=ax2+bx+c(a≠0)的图象和性质想一想,函数y=ax2+bx+c和y=ax2的图象之间的关系是什么？独立作业1.确定下列二次函数的开口方向、对称轴和顶点坐标.;142.22xxy;263.32xxy;21.4xxy.933.5xxy（1）y=3x2+2x342142xxy（7）y=-2x2+8x-8（8）y=-x2-2x结束寄语•探索是数学的生命线.