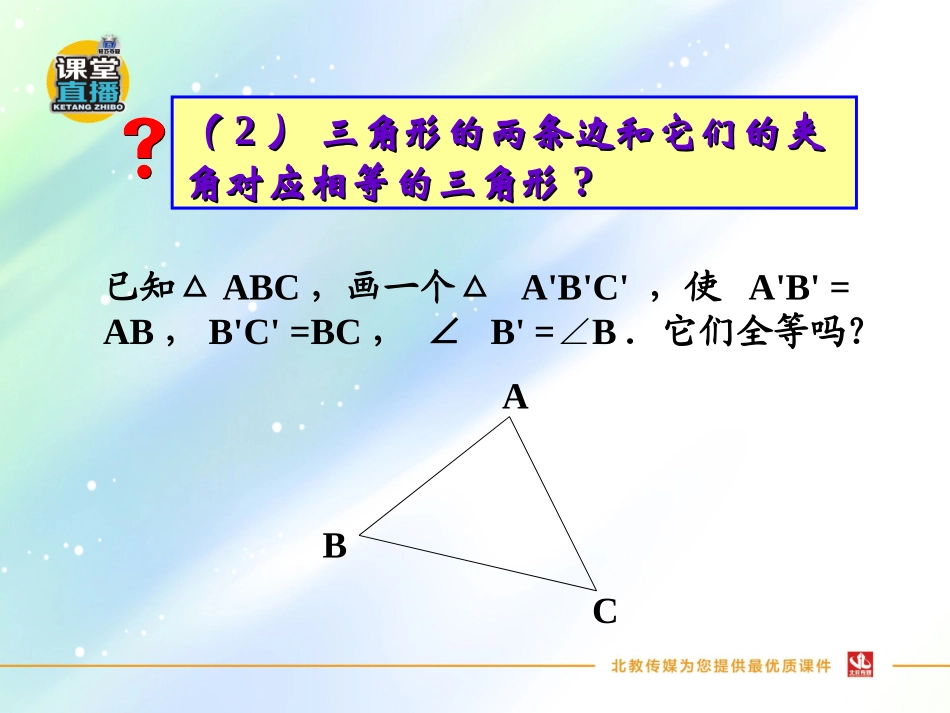
12.2三角形全等的判定第2课时利用两边夹角判定三角形全等11课堂讲解判定两三角形全等的基本事实:边角边全等三角形判定“边角边”的简单应用22课时流程逐点导讲练课堂小结作业提升学习目标学习目标学习目标学习目标((22)三角形的两条边和它们的夹)三角形的两条边和它们的夹角对应相等的三角形角对应相等的三角形??已知△ABC,画一个△A'B'C',使A'B'=AB,B'C'=BC,∠B'=B∠.它们全等吗?ABC1.画∠B’=B∠;2.在射线B’O上截取B’C’=BC,在射线B’F上截取B’A’=BA.3.连接A’C’.以点B为圆心,任意长为半径画弧,分别交BA、BC于点M、N;画一条射线B’O,以点B’为圆心,BM长为半径画弧,交B’O于点P;以点P为圆心,MN长为半径画弧,与上步骤所画的弧交于点Q;过点Q画射线B’F,则∠OB’F=B∠ABCA’B’C’MNOPQF··知识要知识要点点知识要知识要点点““边角边”或“边角边”或“SAS”SAS”两边和它们的夹角对应相等的两个两边和它们的夹角对应相等的两个三角形全等.三角形全等.三角形全等的条件:三角形全等的条件:用符号语言表达为:用符号语言表达为:在△在△ABCABC与△与△DEFDEF中,中,AB=DEAB=DE,,∠∠A=D∠A=D∠,,AC=DFAC=DF,,∴△∴△ABCDEF≌△ABCDEF≌△((SASSAS))..ABC(DEF(例2如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA.连接BC并延长到E,使CE=CB.连接DE,那么量出DE的长就是A、B的距离.为什么?ABCDE证明:在△ABC和△DEC中,CA=CD,∠ACB=DCE∠,CB=CE,∴△ABCDEC≌△(SAS),∴AB=DE.已知:如图,AC=AD,∠CAB=∠DAB,求证:△ACB≌△ADB.证明:在△ACB和△ADB中,AC=AD(已知),∠CAB=∠DAB(已知),AB=AB(公共边),∴△ACB≌△ADB(SAS).ABCD练一练练一练知识要知识要点点知识要知识要点点因为全等三角形的对应角相等,对因为全等三角形的对应角相等,对应边相等,所以,证明分别属于两个三应边相等,所以,证明分别属于两个三角形的线段相等或角相等的问题,常常角形的线段相等或角相等的问题,常常通过证明两个三角形全等来解决.通过证明两个三角形全等来解决.((33)三角形的两个边和其中一个)三角形的两个边和其中一个边的对角对应相等的三角形?边的对角对应相等的三角形?两个边和其中一个边的对角对两个边和其中一个边的对角对应相等的三角形不一定全等.应相等的三角形不一定全等.结论结论结论结论课堂小结判定两三角形全等的基本事实:“边角边”可得两三角形全等角等、线段等条件SAS性质课后作业作业:课本p39练习2T课本p43复习巩固T2,T3