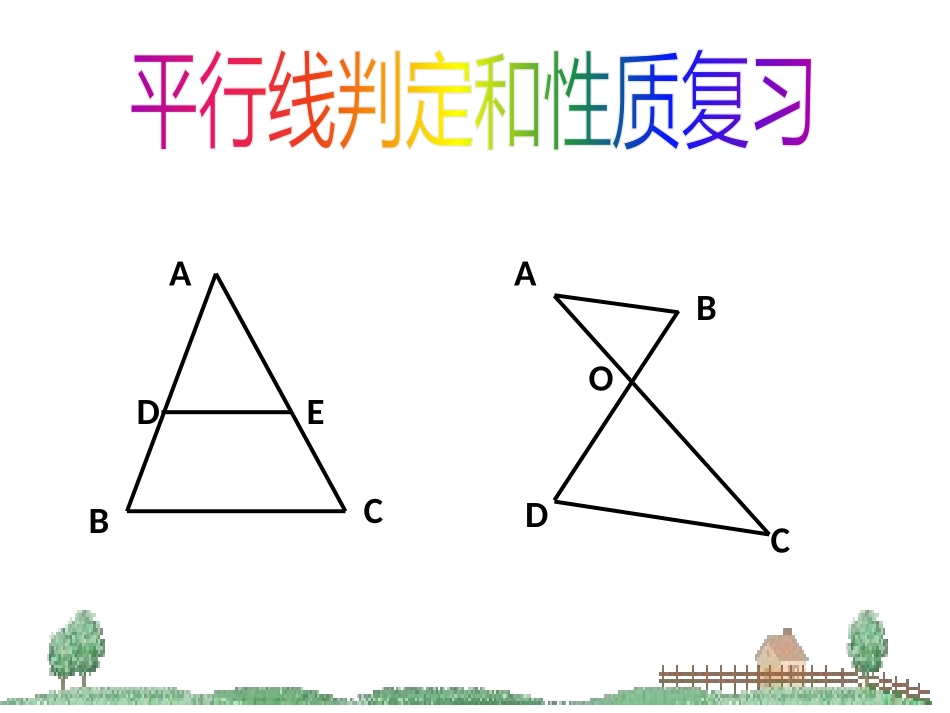
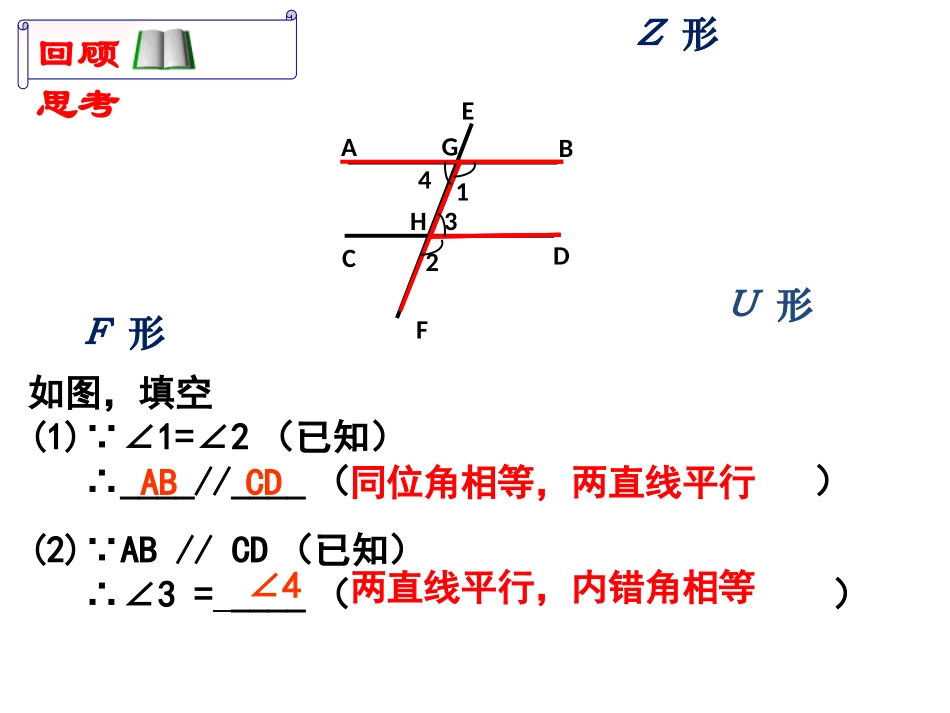
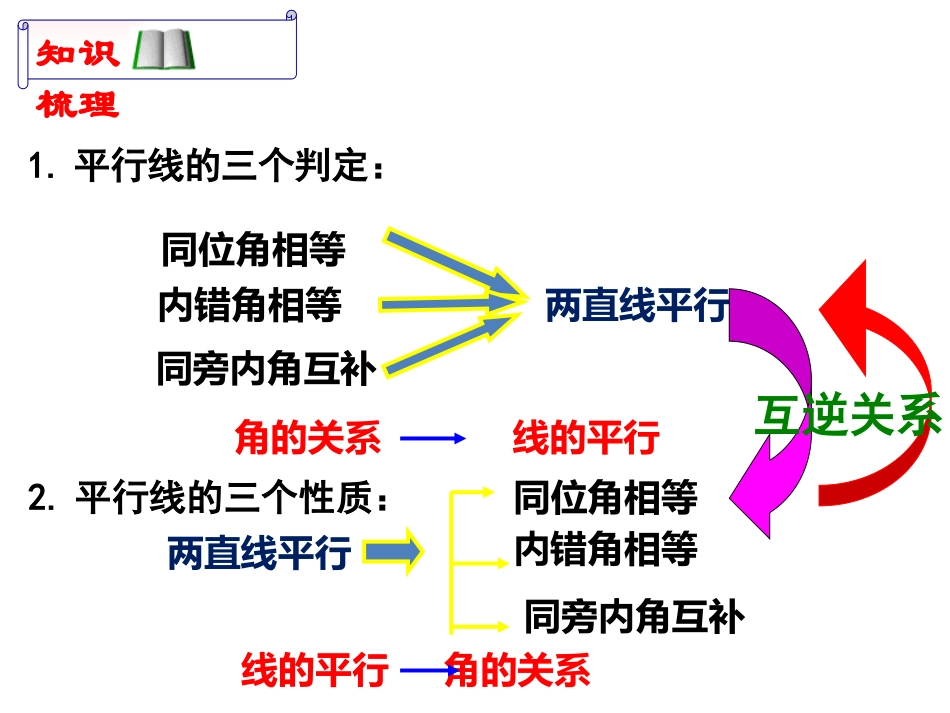
ABCDEABCDOABCDEFHGF形Z形U形如图,填空(1)∵∠1=∠2(已知)∴____//____()3142(2)∵AB//CD(已知)∴∠3=____()同位角相等,两直线平行ABCD两直线平行,内错角相等∠4回顾思考2.平行线的三个性质:两直线平行同位角相等内错角相等同旁内角互补1.平行线的三个判定:两直线平行同位角相等内错角相等同旁内角互补知识梳理角的关系线的平行线的平行角的关系互逆关系ABCDE∵∠ADE=∠B(已知)∴____//____()∴∠AED=()同位角相等,两直线平行DEBC两直线平行,同位角相等∠C问:由DE//BC你还能得到什么结论呢?为什么?∠B+∠BDE=180°∠C+∠CED=180°∵∠B=∠ADE∴DEBC∥∴∠C=∠AED∠B+∠BDE=180°∠C+∠CED=180°角的关系直线平行判定确定其它角的关系性质探索提升∠ADE=∠B,∠AED=∠C如图,已知:试说明:ABCDE如图,已知∠DEC=120°,∠C=60°,∠ADE=65°,求∠B的度数简单应用D如图,已知EF//AB,DEF=B,∠∠试说明DE//BCABCEF分解图形,提炼基本图形从已知到结论,从未知想需知变式:拓展应用请你反思??ABCEFDCEF∵∠B=∠D∴ABCD∥∴∠C=∠A探索提升ABCDO角的关系直线平行判定确定其它角的关系性质∠B=∠D,∠C=∠A吗?如图,如果你能说明如图,AB//CD,∠M=N∠,试说明:∠1=2.∠21ABDCMN拓展应用分解图形,提炼基本图形从已知到结论,从未知想需知请你反思ABCDAMNC变式:如图,AB//CD,∠1=2∠,AMMN⊥,试说明:DNMN⊥.21ABDCMN拓展应用∴∠BAD=∠CDA(两直线平行,内错角相等)解:∵AB//CD(已知)∵∠1=∠2(已知)∴∠BAD-∠1=∠CDA-∠2即∠MAD=∠NDA(等式性质)∴MA//DN(内错角相等,两直线平行)∴∠M=∠N(两直线平行,内错角相等)∵AM⊥MN(已知)∴∠M=90°(垂直的定义)∴∠N=90°(等量代换)∴DN⊥MN(垂直的定义)平行线判定同位角相等内错角相等同旁内角互补两直线平行性质两直线平行同位角相等内错角相等同旁内角互补归纳小结分解图形,提炼基本图形从已知到结论,从未知想需知一、知识整理二、方法小结位置转化思想数量角的关系线的平行线的平行角的关系