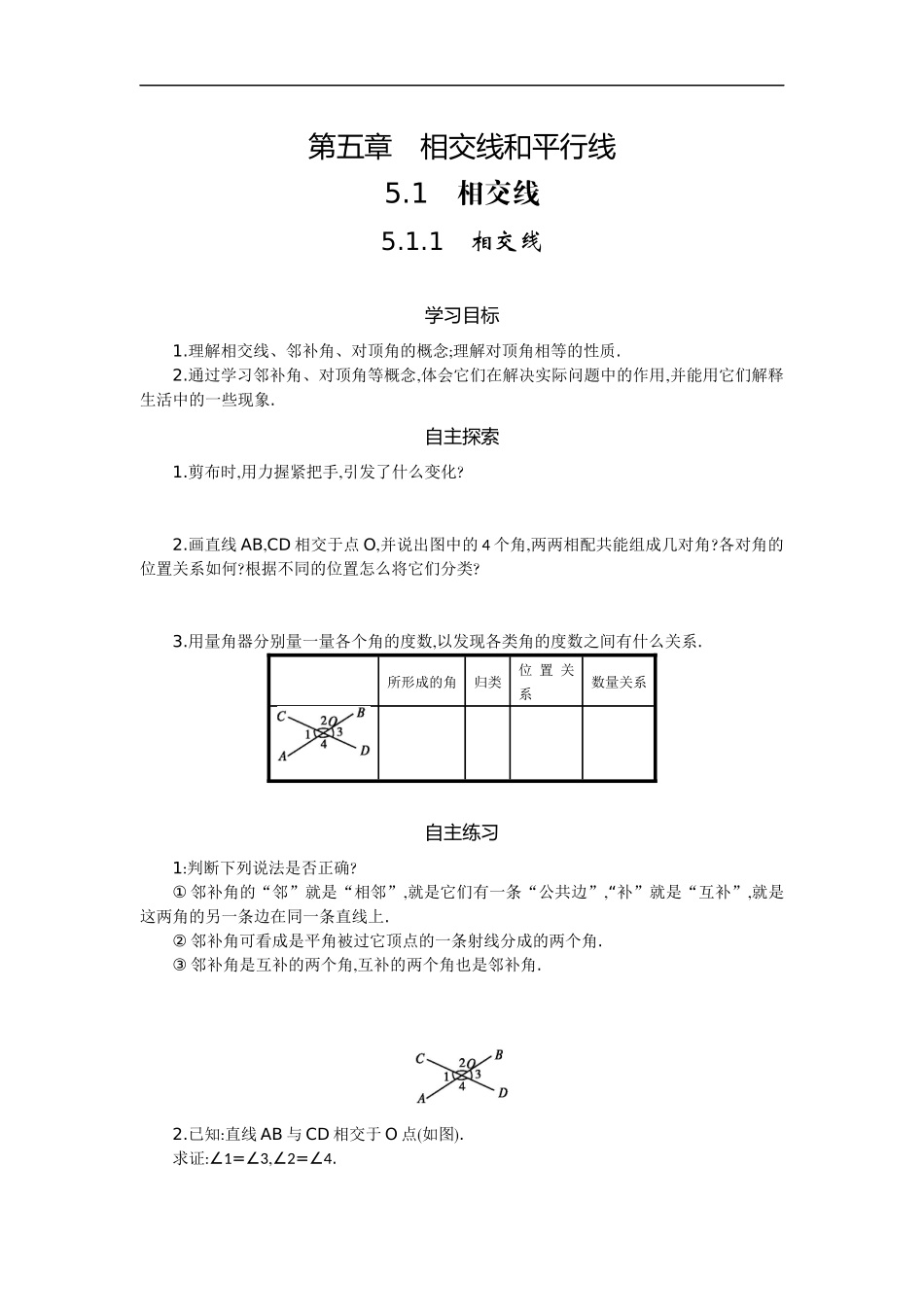
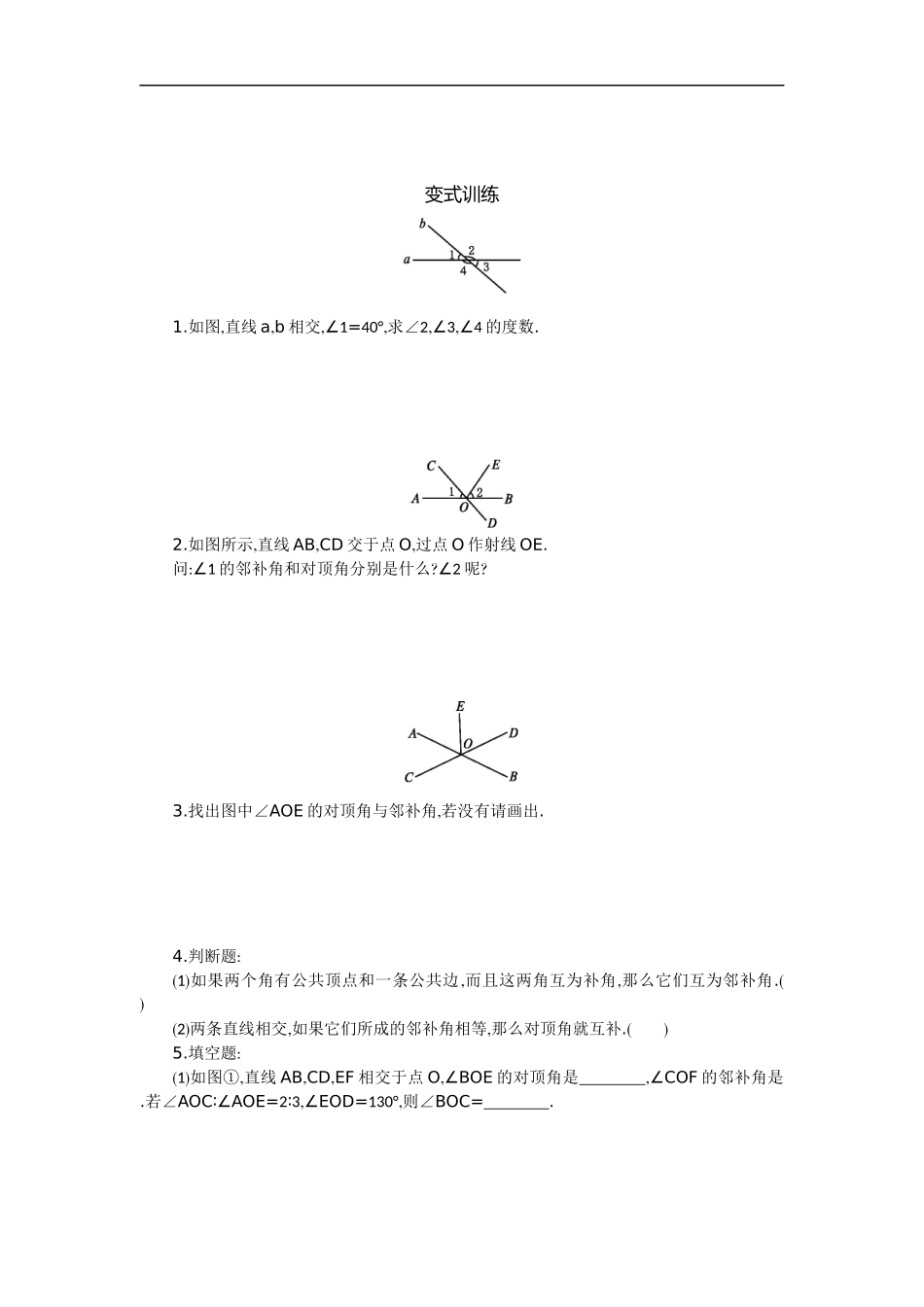
第五章相交线和平行线5.1相交线5.1.1相交线学习目标1.理解相交线、邻补角、对顶角的概念;理解对顶角相等的性质.2.通过学习邻补角、对顶角等概念,体会它们在解决实际问题中的作用,并能用它们解释生活中的一些现象.自主探索1.剪布时,用力握紧把手,引发了什么变化?2.画直线AB,CD相交于点O,并说出图中的4个角,两两相配共能组成几对角?各对角的位置关系如何?根据不同的位置怎么将它们分类?3.用量角器分别量一量各个角的度数,以发现各类角的度数之间有什么关系.所形成的角归类位置关系数量关系自主练习1:判断下列说法是否正确?①邻补角的“邻”就是“相邻”,就是它们有一条“公共边”,“补”就是“互补”,就是这两角的另一条边在同一条直线上.②邻补角可看成是平角被过它顶点的一条射线分成的两个角.③邻补角是互补的两个角,互补的两个角也是邻补角.2.已知:直线AB与CD相交于O点(如图).求证:∠1=∠3,∠2=∠4.变式训练1.如图,直线a,b相交,∠1=40°,求∠2,∠3,∠4的度数.2.如图所示,直线AB,CD交于点O,过点O作射线OE.问:∠1的邻补角和对顶角分别是什么?∠2呢?3.找出图中∠AOE的对顶角与邻补角,若没有请画出.4.判断题:(1)如果两个角有公共顶点和一条公共边,而且这两角互为补角,那么它们互为邻补角.()(2)两条直线相交,如果它们所成的邻补角相等,那么对顶角就互补.()5.填空题:(1)如图①,直线AB,CD,EF相交于点O,∠BOE的对顶角是,∠COF的邻补角是.若∠AOC∶∠AOE=2∶3,∠EOD=130°,则∠BOC=.图①图②(2)如图②,直线AB,CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°,则∠EOF=.达标检测如图所示,直线AB,CD相交于点O.(1)若∠AOC+∠BOD=100°,求各角的度数.(2)若∠BOC比∠AOC的2倍多33°,求各角的度数.