同底数幂的乘法.1..1-同底数幂乘法----VIP免费

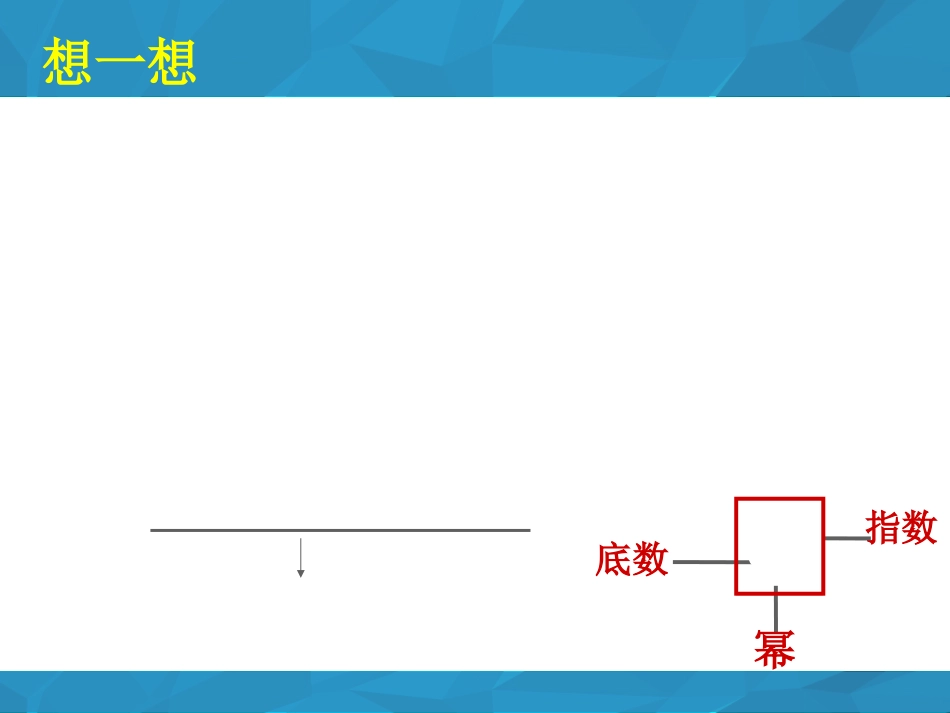
12.1.1同底数幂的乘法想一想1、①a3+a3=2a3②a+a=35a+a35①进行运算的依据是什么？②不能继续进行运算的原因是什么？2、a表示什么意思？可写成什么形式？nan=a•a•a•······•an个a底数an幂指数3、有一种电子计算机，每秒钟可以做10次运算，那么10秒可以做多少次运算呢？83变一变①a•a=33②a•a=35??根据题意，得10×10=83做一做：3210104510103422352232aa65aa1031021010101010个个5101051010101010个幂的定义乘法结合律幂的定义猜一猜：为正整数）、nmaanm?(nmaaanamaaaaaa个个anmaaaa个)(nma幂的意义乘法结合律幂的意义am·an=am+n(m,n都是正整数）同底数幂相乘底数，指数.不变相加同底数幂的乘法运算性质同底数的幂相乘，底数不变，指数相加.式子表述：am·an=am+n(m,n都是正整数）注意问题：（1）底数a可以表示数、字母、代数式；（2）m，n都是正整数；（3）适用条件：①底数相同；②乘法运算；结论：底数不变，指数相加.想一想：（1）当三个或三个以上的同底数幂相乘时，是否也符合上述性质？请你把三个同底数幂相乘的性质用公式表示出来：,,mnpmnpaaaamnp是正整数（2）运算性质反之是否成立？如何表示？逆向应用：是正整数）（nmaaanmnm,例1.计算：（A组）（1）6533（2）471010（3）123xx（4）aa5（B组）（1）532aaa（2）432xxxx62aa62aa3mm1mmyy32babaxyxyyx23（1）（2）（3）（4）（5）（6）（C组）想一想：（1）表示的意义是什么？能否去掉中的括号？为正整数）nan(na－为奇数－为偶数）（nanaannn分类讨论思想（2）与中的“－”号在意义和运算上有什么不同？62aa3mm相反数的符号和底数性质符号；意义上的不同：运算上的不同：一个带进指数运算，另一个不带进指数运算.例2.计算：234xxxx解：原式＝2341xx55xx.25x强调：有同类项要合并同类项（结果要最简），合并时要注意与同底数幂的乘法的区别.巩固练习：1.判断下列各式是否正确？说明理由，并改正：（1）（2）（3）（4）（5）（6）（7）（8）10552aaa1055aaa933bbb6332bbb55aaa65aaa33332xxx62424)(xxxxx×√同底数幂乘法与整式加减的区别：同底数幂乘法：只要求同底数即可，运算时底数不变，指数相加；整式加减：不仅要底数相同，指数也必须相同，实质是合并同类项的过程，“幂不变系数相加”.××××××思考：（1）若，则=；（2）;（3）若，则=；（4）已知,则=_______.28xx9273xx2,3mnaamna72xxxx＝am·an=am+n(m,n都是正整数）同底数幂的乘法性质：底数，指数.不变相加课堂小结同底数的幂相乘，---2015.3.31--思考题：已知：3a2n+m+4an－2m＝7a5求：的值.•(n3m)（m5n）解：由题意，得：2n+m=5n－2m=5解方程组，得：m=－1n=3=m6n46=(－1)•34=81•(n3m)（m5n）