5.3正弦函数的性质-(2)VIP免费

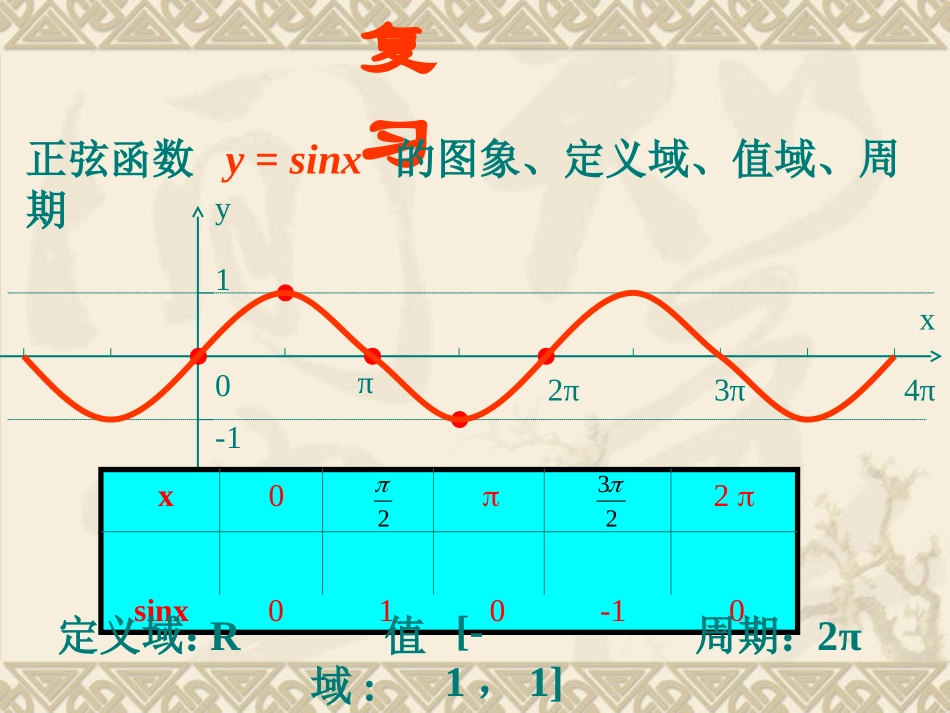
正弦型函数的图象与性质复习正弦函数y=sinx的图象、定义域、值域、周期y0xπ2π1-13π4πx02sinx010-10223定义域：值域:周期：R[-1，1]2π学习目标1、“五点法”画y=Asin(ωx+φ)的图象;2、会用图象变换法由y=sinx得y=Asin(ωx+φ).正弦型函数y＝Asin(ωx＋φ)(A>0,ω>0)|A|为振幅；2T为周期；为频率21Tfx为相位，称为初相1、A的作用：研究y=Asinx与y=sinx图象的关系先观察y=2sinx、y=sinx与y=sinx的图象间的关系21y0xπ2π12-1-2xsinx2sinxsinx21010-10020-2001/20-1/200π2π223y0xπ2π12-1-2A的作用：使正弦函数的振幅发生变化。y=Asinx（A>0,A1)的图象是由y=sinx的图象沿y轴方向伸长(当A>1时)或缩短（当00,ω1)的图象是由y=sinx的图象沿x轴缩短(当ω>1时)或伸长（当0<ω<1时)到原来的ω-1倍而成.先观察y=sin2x、y=sinx与y=sinx的图象间的关系2、ω的作用：研究y=sinωx与y=sinx图象的关系213、将函数y=sin2x的横坐标伸长为原来的4倍得到（）Ay=sinxBy=sin4xCy=sin(x/2)Dy=sin8x横坐标缩短到原来的1/4倍解：最大值是1，最小值是－1，最小正周期T=8π。1、y=sinxy=sin4x横坐标伸长到原来的4倍C跟踪练习2、求函数y=sin的最大值、最小值和最小正周期。4xy0xπ2π1-13、的作用：研究y=sin(x+)与y=sinx图象的关系与y=sinx的图象间的关系先观察y=sin（x+）、y=sin（x－）433x4x)3sin(x)4sin(x2232022320010100101035673263x494745434xy0xπ2π1-1的作用：使正弦函数的图象发生左右平移（相位变化）y=sin(x+)（0)的图象是由y=sinx的图象向左（>0)或向右(<0)平移∣∣个单位而成.3、的作用：研究y=sin(x+)与y=sinx图象的关系与y=sinx的图象间的关系先观察y=sin（x+）、y=sin（x－）43342232、将函数y=sinx图象向左平移1个单位，再向右平移3个单位，可以得到函数（）的图象。（A）y=sin(x＋2)（B）y=sin(x－2)（C）y=sin(x＋4)（D）y=sin(x－4)1、y=sinxB跟踪练习y=sin(x+)6图像向左平移个单位6图像向右平移个单位6y=2sinxy=sinxy=sinxy0xπ2π12-1-221y0xπ2π3π4π1-1y=sin2xy=sinxy=sinx21y0xπ2π1-1y=sin（x＋）y=sin（x－）y=sinx43ωA34周期变换振幅变换相位变换π37π12-33yxoπ125π6-π6思考：作函数y=3sin(2x+)简图并讨论此图象是由y=sinx图像怎样变换得到的。32232032x651273126x03030)32sin(3xy纵坐标不变横坐标变为原来1/2xy=sinxy=3sin2xy=3sinxyo横坐标不变纵坐标变为原来的3倍角度一：)32sin(3xy图象向左平移个单位6纵坐标不变横坐标变为原来的1/2横坐标不变纵坐标变为原来的3倍xy=sinxyo图像向左平移角度二：)3sin(xy)32sin(xy个单位3)32sin(3xy2、纵坐标变为原来的A倍，横坐标不变；一、正弦型函数y=Asin(ωx+)的图象可以将y=sinx的图象怎样变换得到）（0,0A1、横坐标变为原来的倍，纵坐标不变...