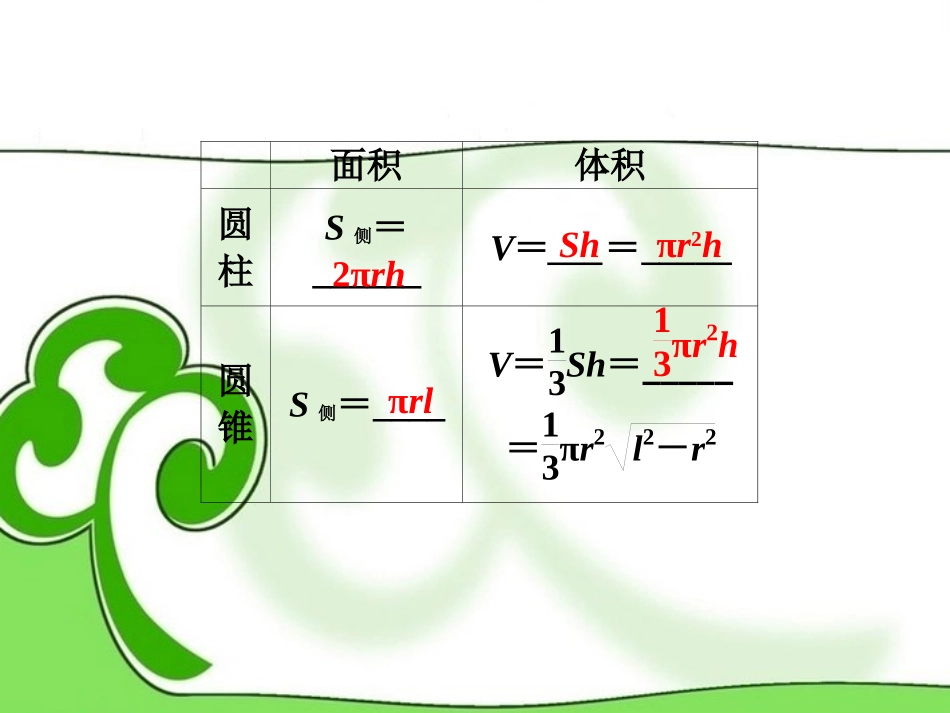
第2课时空间几何体的表面积和体积基础梳理柱、锥、台和球的侧面积和体积教材回扣夯实双基面积体积圆柱S侧=______V=___=_____圆锥S侧=____V=13Sh=_____=13πr2l2-r22πrhShπr2hπrl13πr2h面积体积圆台S侧=________V=13(S上+S下+S上·S下)h=13π(r21+r22+r1r2)h直棱柱S侧=____V=____π(r1+r2)lChSh面积体积正棱锥S侧=_______V=______正棱台S侧=__________V=13(S上+S下+S上·S下)h球S球面=______V=______4πR212Ch′13Sh43πR312(C+C′)h′课前热身1.已知某球的体积大小等于其表面积大小,则此球的半径是()A.3B.3C.4D.5解析:选B.设球半径为R,则43πR3=4πR2,∴R=3.2.若某几何体的三视图(单位:cm)如图所示,则此几何体的侧面积等于()A.12πcm2B.15πcm2C.24πcm2D.30πcm2解析:选B.由三视图可知该几何体是圆锥,其底面半径为3,母线长l=5,∴S侧=π×3×5=15π(cm2).3.(2011·高考福建卷)三棱锥P-ABC中,PA⊥平面ABC,PA=3,底面ABC是边长为2的正三角形,则三棱锥P-ABC的体积等于________.解析: PA⊥底面ABC,∴PA为三棱锥P-ABC的高,且PA=3. 底面ABC为正三角形且边长为2,∴底面面积为12×22×sin60°=3,∴VP-ABC=13×3×3=3.答案:34.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是________.解析:此几何体的上部为球,球的直径为2,下部为一圆柱,圆柱的高为3,底面圆的直径为2,所以S表=4π+π+π+2π×3=12π.答案:12π考点探究讲练互动考点突破考点突破(2011·高考北京卷)某四棱锥的三视图如图所示,该四棱锥的表面积是()例例11几何体的表面积A.32B.16+162C.48D.16+322【解析】由三视图还原几何体的直观图如图所示.S表=12×4×22×4+4×4=16+162.【答案】B【题后感悟】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.备选例题(教师用书独具)(2011·高考四川卷)如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是________.例例【解析】法一:圆柱的轴截面如图所示,设球的半径与圆柱的高所成的角为α,则圆柱底面半径为4sinα,高为8cosα,∴S圆柱侧=2π·4sinα·8cosα=32πsin2α.当sin2α=1时,S圆柱侧最大为32π.此时S球表-S圆柱侧=4π·42-32π=32π.法二:设圆柱底面半径为r,则其高为2R2-r2,∴S圆柱侧=2πr·2R2-r2=4πr2R2-r2≤4πr2+R2-r22=2πR2当且仅当r2=R2-r2,即r=22R时取“=”.又R=4,∴S圆柱侧最大为32π.此时S球表-S圆柱侧=4π·42-32π=32π.【答案】32π变式训练1.一个几何体的三视图如图所示,则该几何体的表面积为()A.(2+5)πB.(3+5)πC.6πD.(2+6)π解析:选A.该几何体的直观图为上面是一个圆锥,下面是一个同底的圆柱,如图所示.该几何体的表面积为S=2π+π+4π=(2+5)π,故选A.(2011·高考天津卷)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.例例22几何体的体积【答案】6+π【解析】此几何体是由一个长为3,宽为2,高为1的长方体与底面直径为2,高为3的圆锥组合而成的,故V=V长方体+V圆锥=3×2×1+×12×3=(6+π)m3.【题后感悟】给出几何体的三视图,求该几何体的体积或表面积时,可以根据三视图还原出实物,画出该几何体的直观图,确定该几何体的结构特征,并利用相应的体积公式求出其体积,求体积的方法有直接套用公式法、等体积转换法和割补法等多种.若所给几何体为不规则几何体,常用等积转换法和割补法求解.备选例题(教师用书独具)一个几何体是由圆柱ADD1A1和三棱锥E-ABC组合而成的,点A、B、C在圆O的圆周上,其正视图、侧视图的面积分别为10和12,如图所示,其中EA⊥平面ABC,AB⊥AC...