用等式的性质解方程VIP免费

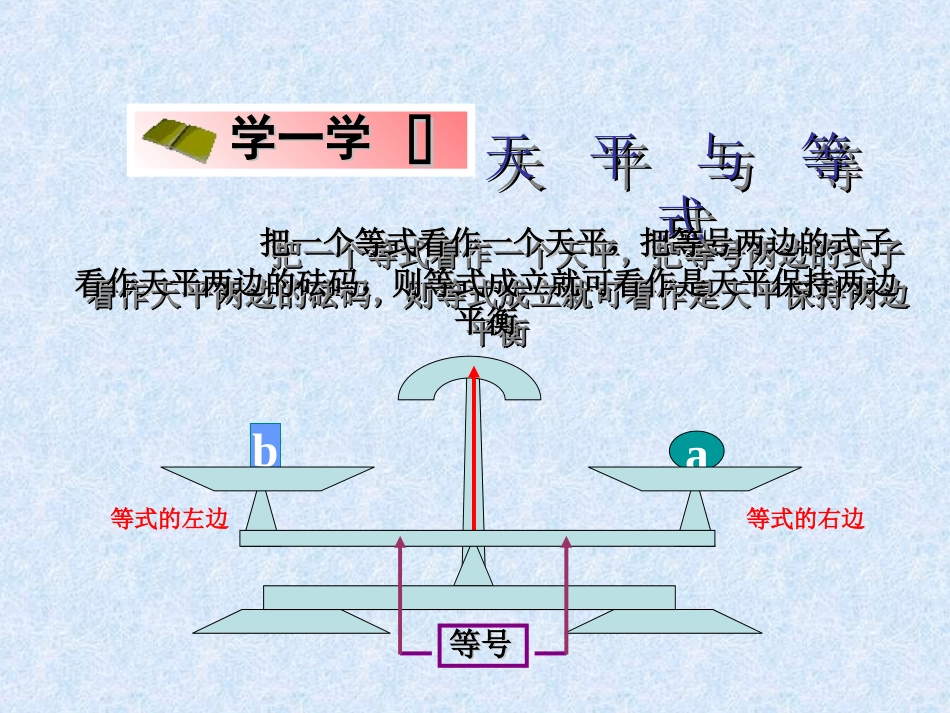
利用等式的性质解方程获嘉县实验学校樊玲ba学一学学一学天平与等天平与等式式天平与等天平与等式式把一个等式看作一个天平，把等号两边的式子把一个等式看作一个天平，把等号两边的式子看作天平两边的砝码，则等式成立就可看作是天平保持两边看作天平两边的砝码，则等式成立就可看作是天平保持两边平衡平衡把一个等式看作一个天平，把等号两边的式子把一个等式看作一个天平，把等号两边的式子看作天平两边的砝码，则等式成立就可看作是天平保持两边看作天平两边的砝码，则等式成立就可看作是天平保持两边平衡平衡等式的左边等式的右边等号等号a你能发现什么规律？你能发现什么规律？右左a你能发现什么规律？你能发现什么规律？右左a你能发现什么规律？你能发现什么规律？右左ab你能发现什么规律？你能发现什么规律？右左ba你能发现什么规律？你能发现什么规律？右左ba你能发现什么规律？你能发现什么规律？a=b右左ba你能发现什么规律？你能发现什么规律？a=bc右左cba你能发现什么规律？你能发现什么规律？a=b右左acb你能发现什么规律？你能发现什么规律？a=b右左cbca你能发现什么规律？你能发现什么规律？a=b右左cbca你能发现什么规律？你能发现什么规律？a=ba+cb+c=右左cc你能发现什么规律？你能发现什么规律？a=bab右左c你能发现什么规律？你能发现什么规律？a=bab右左c你能发现什么规律？你能发现什么规律？a=bab右左你能发现什么规律？你能发现什么规律？a=bba右左你能发现什么规律？你能发现什么规律？a=ba-cb-c=ba右左等式性质1：等式两边加（或减）同一个数（或式子），结果仍相等。，那么____b___a如果baccba你能发现什么规律？你能发现什么规律？a=b右左ba你能发现什么规律？你能发现什么规律？a=b右左ab2a=2bba你能发现什么规律？你能发现什么规律？a=b右左bbaa3a=3bba你能发现什么规律？你能发现什么规律？a=b右左bbbbbbaaaaaaC个C个ac=bcba你能发现什么规律？你能发现什么规律？a=b右左22ba33bacbca)0(c等式性质2：等式两边乘同一个数，或除以同一个不为0的数，结果仍相等。______ba，那么b____a___如果ba，那么如果,ba0ccccc等式的性质等式的性质等式的性质等式的性质cbcaba，那么如果【等式性质2】bcacba，那么如果cbcacba那么如果,0【等式性质１】注意注意1、等式两边都要参加运算，并且是作同一种运算。2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。3、等式两边不能都除以0，即0不能作除数或分母.等式的性质1：等式两边加(或减)同一个数（或式子子），结果仍相等。等式的性质2：等式两边乘同一个数，或除以同一个不为0数，结果仍相等。等式的两个性质(1)如果x=y,那么（）(2)如果x=y,那么（）(3)如果x=y,那么（）(4)如果x=y,那么（）(5)如果x=y,那么（）判断对错，对的说明根据等式的哪一条性质；错的说出为什么。a5ya5x31y231x2a5ya5xy5x532y32x×√××√应用例1：用适当的数或整式填空，使所得结果仍是等式，并说明是根据等式的哪一条性质以及怎样变形（改变式子的形状）的。①、如果2x=5-3x，那么2x+（）=5②、如果0.2x=10，那么x=（）解：①、2x+（3x）=5根据等式性质1，等式两边都加上3x。②、x=(50)根据等式性质2，等式两边都除以0.2或乘以5。+2+244x43=练习1:填空①若x－2=3，根据__________，得到x－2=3，即x=5。②若－4x=3，根据___________，得到,即x=____。等式的性质1等式的性质243所以解一元一次方程就是利用等式的性质质把方程转化为x=a(常数）的形式例2：利用等式的性质解下列方程267(1)x205(2)x-解：两边减7，得于是72677x19x解：两边除以-5，得5205-5x-于是4x例2：利用等式的性质解下列方程4531(3)x解：两边加5，得化简，得545531x931x两边同乘-3，得27x检验：将27x代入方程4531x，得：左边52731459右边所以27x是方程的解。4531(3)x解：两边加5，得化简，得545531x931x两边同乘-3，得27x解：两边同乘-3，得...