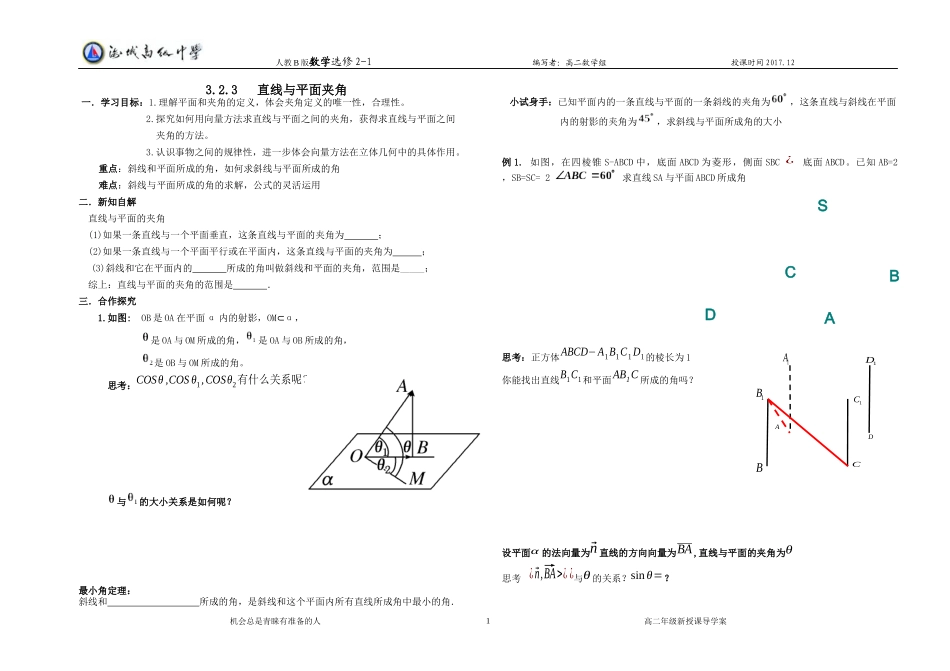
BADSABCD1A1B1C1D人教B版数学选修2-1编写者:高二数学组授课时间2017.123.2.3直线与平面夹角一.学习目标:1.理解平面和夹角的定义,体会夹角定义的唯一性,合理性。2.探究如何用向量方法求直线与平面之间的夹角,获得求直线与平面之间夹角的方法。3.认识事物之间的规律性,进一步体会向量方法在立体几何中的具体作用。重点:斜线和平面所成的角,如何求斜线与平面所成的角难点:斜线与平面所成的角的求解,公式的灵活运用二.新知自解直线与平面的夹角(1)如果一条直线与一个平面垂直,这条直线与平面的夹角为;(2)如果一条直线与一个平面平行或在平面内,这条直线与平面的夹角为;(3)斜线和它在平面内的所成的角叫做斜线和平面的夹角,范围是_____;综上:直线与平面的夹角的范围是.三.合作探究1.如图:OB是OA在平面α内的射影,OMα⊂,是OA与OM所成的角,是OA与OB所成的角,是OB与OM所成的角。思考:COSθ,COSθ1,COSθ2有什么关系呢?与的大小关系是如何呢?最小角定理:斜线和所成的角,是斜线和这个平面内所有直线所成角中最小的角.小试身手:已知平面内的一条直线与平面的一条斜线的夹角为,这条直线与斜线在平面内的射影的夹角为,求斜线与平面所成角的大小例1.如图,在四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC¿底面ABCD。已知AB=2,SB=SC=2求直线SA与平面ABCD所成角思考:正方体ABCD−A1B1C1D1的棱长为1你能找出直线B1C1和平面AB1C所成的角吗?设平面α的法向量为⃗n直线的方向向量为BA,直线与平面的夹角为θ思考¿⃗n,⃗BA>¿¿与θ的关系?sinθ=?机会总是青睐有准备的人高二年级新授课导学案C1⃗nBA⃗nBA⃗nBA⃗nBA⃗nAB⃗nAB⃗nAB⃗nABABCD1A1B1C1DDD1C1A1EFABCB1人教B版数学选修2-1编写者:高二数学组授课时间2017.12例2:正方体ABCD−A1B1C1D1的棱长为1四.课后作业1.(2015全国2),长方体ABCD−A1B1C1D1中,,点E,F分别在上,,过点E,F的平面α与此长方体的面相交,交线围成一个正方形。(1)在图中画出这个正方形(不必说明画法和理由);(2)求直线AF与平面α所成的角的正弦值。2.在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.(1)求证:PB⊥DM;(2)求BD与平面ADMN所成的角机会总是青睐有准备的人高二年级新授课导学案111.BCABC求与面所成的角2