2.3.4平面与平面垂直的性质VIP免费

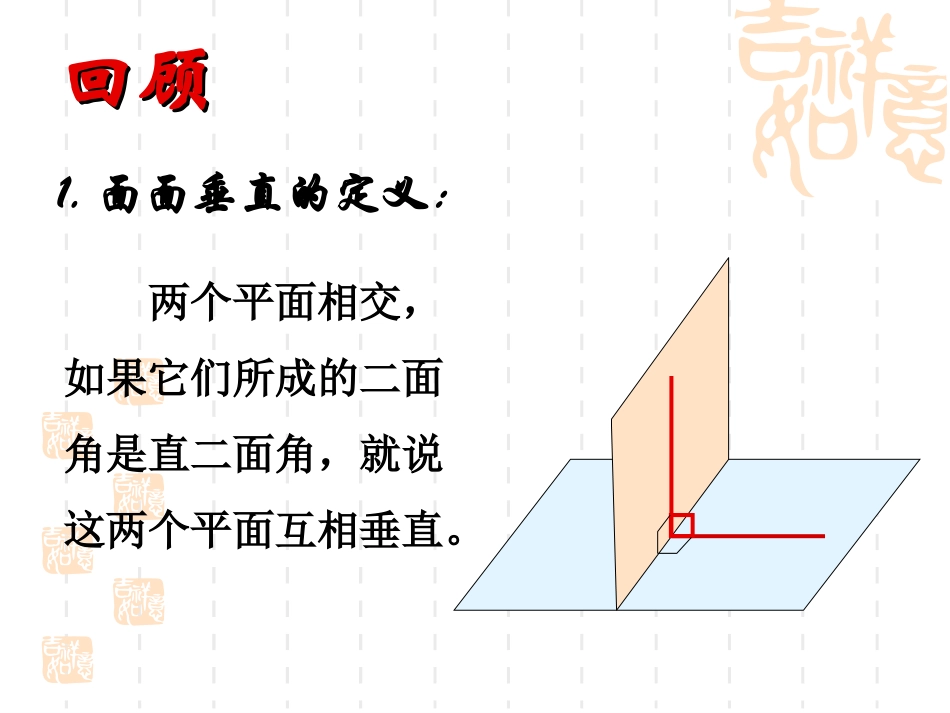
2.3.4平面与平面垂直的性质回顾回顾1.面面垂直的定义：两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直。回顾回顾2.面面垂直的判定定理：一个平面过另一个平面的垂线，则这两个平面垂直。aaaA1D1B1C1CBAD面面垂直的性质αβ如果α⊥β(1)α里的直线都和β垂直吗？DEF(2)什么情况下α里的直线和β垂直？探究探究.,,,BCDABABCD于已知.:AB求证则∠ABE就是二面角-CD-的平面角∵,ABBE(∴⊥平面与平面垂直的定义)又由题意知ABCD,⊥且BECD=BE证明:在平面内作BECD,⊥垂足为B.∴AB⊥(直线与平面垂直的判定定理)DCAB面面垂直的性质面面垂直性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。面面垂直线面垂直αβaAllaalabbβαPa思考：设平面⊥平面，点P在平面内，过点P作平面的垂线a，直线a与平面具有什么位置关系?βαPa直线a在平面内例4,,,aaa判断与位置关系解：设αβallb在α内作直线b⊥llbblba又//abba//aP73A组第5题αβlγabmn在α内作直线a⊥n证法1：设，,nm在β内作直线b⊥mnaanab同理//baab//bbl//blb面面垂直性质线面平行判定线面平行性质lab在γ内过A点作直线a⊥n，证法2：设，,nm在γ内过A点作直线b⊥m，αβlγnmAnaanallalb同理Abal思考：思考：还可以怎样作辅助线？在γ内任取一点A（不在m,n上），解法分析：1.两种证法的共同点是：都从一个面内做交线的垂线，目的是使用面面垂直的性质定理。2.证法2比证法1巧妙、简捷。原因是在考虑到了面面垂直的条件的同时还考虑了结论：线面垂直。因此，两条线作在γ内更有利。规律小结：一、怎样证线线平行：1.利用平面几何中的定理：三角形（或梯形）的中位线与底边平行、平行四边形的对边平行、利用比例、……2.利用公理4:3.利用线面平行的性质定理：如果一条直线平行于一个平面，经过这条直线的平面和这个平面相交，则这条直线和交线平行4.利用面面平行的性质定理：5.利用线面垂直的性质定理：如果两个平行平面同时和第三个平面相交，那么它们的交线平行，平行于同一条直线的两条直线互相平行垂直于同一个平面的两条直线平行二、怎样证线线垂直：1.利用平面几何中的定理：半圆上的圆周角是直角、勾股定理的逆定理……2.利用平移：3.利用线面垂直定义：a⊥b,b∥c，则a⊥ca⊥α,bα，则a⊥b4.利用三垂线定理或其逆定理；