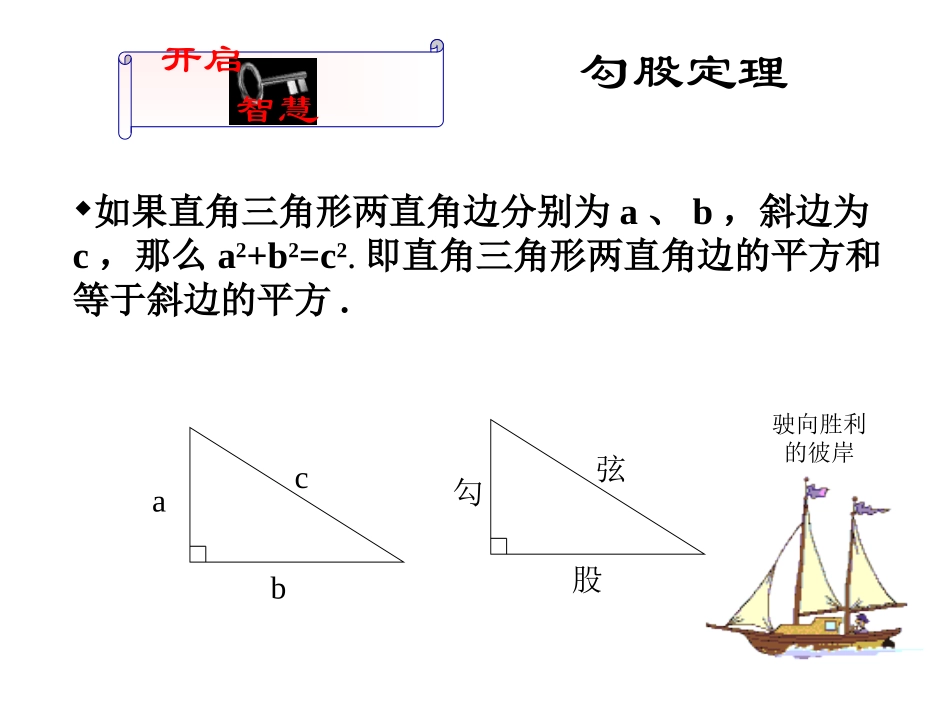
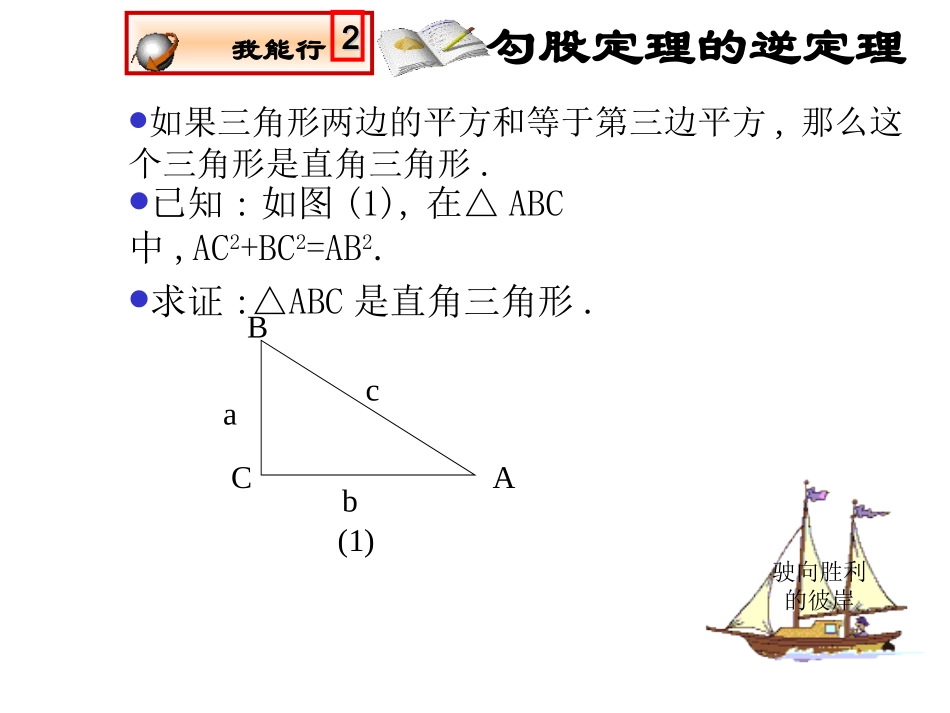
九年级数学(上册)第一章三角形的证明•2.直角三角形(1)•勾股定理与它的逆定理的证明开启智慧勾股定理如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方.acb勾弦股驶向胜利的彼岸我能行22勾股定理的逆定理如果三角形两边的平方和等于第三边平方,那么这个三角形是直角三角形.已知:如图(1),在△ABC中,AC2+BC2=AB2.求证:△ABC是直角三角形.acbABC(1)驶向胜利的彼岸证明:作Rt△A′B′C′使∠C′=900,A′C′=AC,B′C′=BC(如图),则已知:如图(1),在△ABC中,AC2+BC2=AB2.求证:△ABC是直角三角形.A′C′2+B′C′2=A′B′2(勾股定理).∵AC2+BC2=AB2(已知),A′C′=AC,B′C′=BC(作图),∴AB2=A′B′2(等式性质).∴AB=A′B′(等式性质).∴△ABC≌△A′B′C′(SSS).∴∠A=A∠′=900(全等三角形的对应边).∴△ABC是直角三角形(直角三角形意义).我能行22逆定理的证明acbABC(1)acbB′A′C′(2)回顾反思11驶向胜利的彼岸勾股定理的逆定理如果三角形两边的平方和等于第三边平方,那么这个三角形是直角三角形.这是判定直角三角形的根据之一.在△ABC中∵AC2+BC2=AB2(已知),∴△ABC是直角三角形(如果三角形两边的平方和等于第三边平方,那么这个三角形是直角三角形).acbABC(1)几何的三种语言开启智慧命题与逆命题直角三角形两直角边的平方和等于斜边的平方.如果三角形两边的平方和等于第三边平方,那么这个三角形是直角三角形观察上面两个命题,它们的条件与结论之间有怎样的关系?与同伴交流.再观察下面三组命题:如如果两个角是对顶角,那么它们相等,如如果两个角相等,那么它们是对顶角;如如果小明患了肺炎,那么他一定会发烧,如如果小明发烧,那么他一定患了肺炎;上面每组中两个命题的条件和结论之间也有类似的关系吗?与同伴进行交流.开启智慧在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.你能写出命题“如果两个有理数相等,那么它们的平方相等”的逆命题吗?它们都是真命题吗?想一想:一个命题是真命题,它逆命题是真命题还是假命题?驶向胜利的彼岸一个命题是真命题,它逆命题却不一定是真命题.我们已经学习了一些互逆的定理,如:勾股定理及其逆定理,两直线平行,内错角相等;内错角相等,两直线平行.你还能举出一些例子吗?想一想:互逆命题与互逆定理有何关系?如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.开启智慧定理与逆定理蓄势待发隋堂练习11驶向胜利的彼岸老师提示:你是否能将有关命题的知识予以整理.四四边形是多边形;两两直线平行,同旁内角互补;如如果ab=0,那么a=0,b=0.请你举出一些命题,然后写出它的逆命题,并判断这些逆命题的真假.1.如图(单位:厘米),在一个长方体的房间里,一只蜘蛛在一面墙的正中间离天花板100厘米的A处,苍蝇则在对面墙的正中间离地板100厘米的B处.试问:蜘蛛为了捕获苍蝇,需要爬行的最短距离是多少?●AB●500300300梦想成真试一试P1422回味无穷•勾股定理:如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2.即直角三角形两直角边的平方和等于斜边的平方..•勾股定理的逆定理:如果三角形两边的平方和等于第三边平方,那么这个三角形是直角三角形.•命题与逆命题在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题.•定理与逆定理如果一个定理的逆命题经过证明是真命题,那么它是一个定理,这两个定理称为互逆定理,其中一个定理称另一个定理的逆定理.小结拓展知识的升华祝你成功!独立作业结束寄语下课了!•严格性之于数学家,犹如道德之于人.•证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.