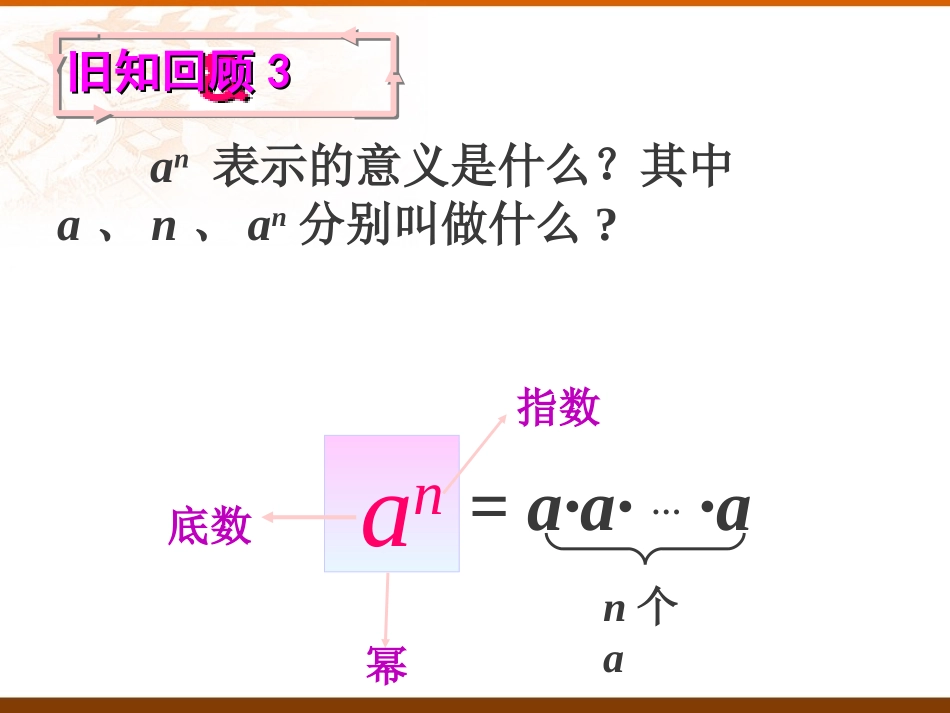
旧知回顾旧知回顾33=a·a·…·an个aan表示的意义是什么?其中a、n、an分别叫做什么?an底数幂指数14.2.1同底数幂的乘法14.1.2幂的乘方问题:一种电子计算机每秒可进行次运算,它工作秒可进行多少次运算?=(10×···×10)×(10×10×10)新知探究114个10=(10×10×···×10)17个10=101710141033个101014×103解:新知探究新知探究22(1)25×22=()×()=________________=2();(2)a3×a2=()×()=_______________=a();(3)5m·5n=()×()=5().2×2×2×2×22×22×2×2×2×2×2×27a×a×aa×aa×a×a×a×a5m+n请同学们根据乘方的意义理解,完成下列填空.5×···×5m个5n个55×···×5(m+n)个5am·an=m个an个a=a·a…a=am+n.(m+n)个a同底数幂相乘,底数不变,指数相加即am·an=am+n(m、n都是正整数)(a·a…a)(a·a…a)同底数幂的乘法法则:条件:①乘法②同底数幂结果:①底数不变②指数相加总结规律:对于任意底数a与任意整正整数m、n有:练习下面的计算对不对?如果不对,怎样改正?(1)b5·b5=2b5()(2)b5+b5=b10()(3)x5·x5=x25()(4)y5·y5=2y10()(5)c·c3=c3()b5·b5=b10b5+b5=2b5x5·x5=x10y5·y5=y10c·c3=c4×××××Areyouclear?例1计算下列各式,结果用幂的形式表示.(2)a·a6;21+4+3a1+6xm+3m+1(1)x2·x5;例题赏析:(4)xm·x3m+1;x2+5=x7(3)2×24×23==28(2)a·a6==a7(3)2×24×23;(4)xm·x3m+1==y4m+1解(1)x2·x5=am·an·ap=am+n+p(m、n、p都是正整数)通过领悟例题由(3)思考:(当m、n、p都是正整数时)am·an·ap=?顺用公式:am·an=am+n(m、n都是正整数)逆用公式:am+n=am·an(m、n都是正整数)填空:(1)x5·()=x8(2)a·()=a6(3)x·x3()=x7(4)xm·()=x3m变式训练x3a5x3x2m真棒!真不错!你真行!太棒了!am·an=am+n(m,n都是正整数).同底数幂的乘法性质:底数指数.不变相加幂的意义:an=a·a·…·an个a注意:同底数幂相乘时,你在知识上有哪些收获,你学到了哪些方法?am·an·ap=am+n+p(m、n、p都是正整数).逆用公式:am+n=am·an(m、n都是正整数)manmmmnmaaaa个)(mnmmma个?)(nma对于任意底数a与任意正整数m,n,mna(乘方的意义)(同底数幂的乘法法则)(乘法的定义)mnnmaa)((m,n都是正整数).幂的乘方,底数,指数.不变相乘幂的乘方的运算公式你能用语言叙述这个结论吗?公式中的a可表示一个数、字母、式子等.例2:计算:(1)(103)5;(2)(a4)4;(3)(am)2;(4)-(x4)3.解:(1)(103)5=103×5=1015;(2)(a4)4=a4×4=a16;(3)(am)2=am×2=a2m;(4)-(x4)3=-x4×3=-x12.活动3计算:(1)(103)3;(2)(x3)2;(3)-(xm)5;(4)(a2)3∙a5;⑸23)(y⑹43])[(ba运算种类公式法则中运算计算结果底数指数同底数幂乘法幂的乘方乘法乘方不变不变指数相加指数相乘mnnmaa)(nmnmaaa活动4下列各式对吗?请说出你的观点和理由:(1)(a4)3=a7()(2)a4a3=a12()(3)(a2)3+(a3)2=(a6)2()(4)(-x3)2=(-x2)3()××××××××活动51.下列各式中,与x5m+1相等的是()(A)(x5)m+1(B)(xm+1)5(C)x·(x5)m(D)x·x5·xmc2.x14不可以写成()(A)x5·(x3)3(B)(-x)·(-x2)·(-x3)·(-x8)(C)(x7)7(D)x3·x4·x5·x2C活动6幂的乘方的逆运算:(1)x13·x7=x()=()5=()4=()10;(2)a2m=()2=()m(m为正整数).20x4x5x2ama2mnnmmnaaa)()(幂的乘方法则的逆用活动7已知,44•83=2x,求x的值.9822172334234)2()2(84解:17x所以活动81.已知3×9n=37,求:n的值.2.已知a3n=5,b2n=3,求:a6nb4n的值.3.设n为正整数,且x2n=2,求9(x3n)2的值.4.已知2m=a,32n=b,求:23m+10n.