2.2.1对数与对数运算(第一课时——对数及对数的性质)VIP免费

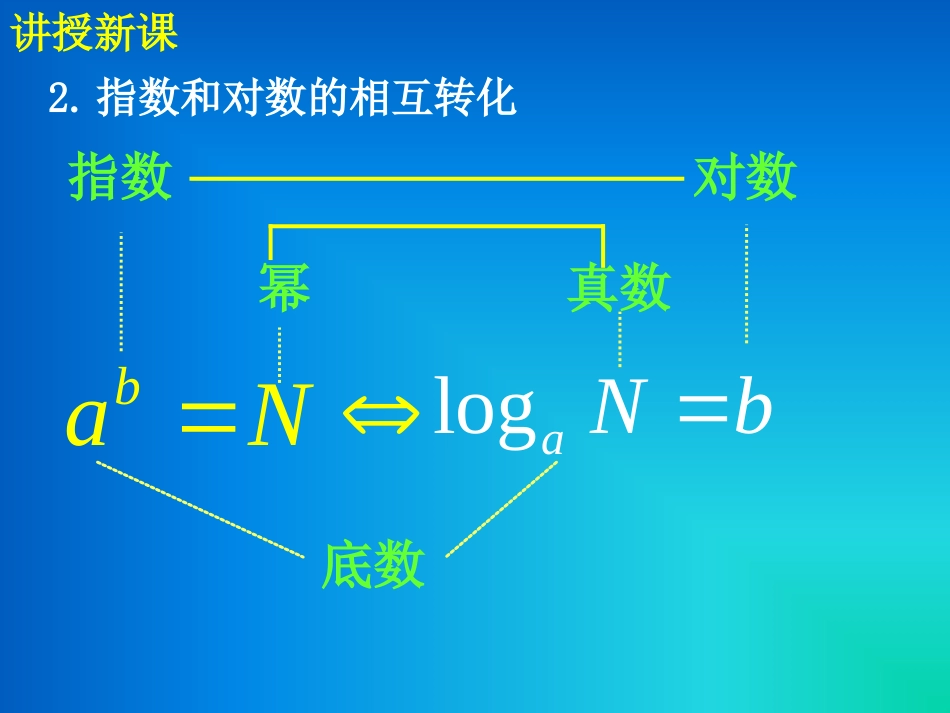
2.2.1对数与对数的运算(第一课时)其中a叫做对数的底数,N叫做真数.1.对数的定义：一般地，如果ax=N(a>0,且a≠1)那么数x叫做以a为底N的对数，ax=logN记作:讲授新课注意：限制条件是a>0,且a≠1baNlogaNb底数幂真数指数对数2.指数和对数的相互转化讲授新课3.两个重要的对数：(1)常用对数：以10为底的对数。简记作。如简记为10logNlgN(2)自然对数：以无理数e=2.71828…为底的对数。简记作。如简记为elogNlnN讲授新课10log3.5log9elg3.5.ln9.例1．将下列指数式写成对数式：5.73)31((4)2710(3)b1e(2)6255(1)ma64解：例题分析(练习：课本P641)11(2)logln6ebb10(3)log27lg27a5(1)log625413(4)log5.73m例2．将下列对数式写成指数式：12(1)log1642(2)log1287(3)lg0.012(4)ln102.303(1)411627(2)21282(3)100.012.303(4)10e解：例题分析(练习：课本P642)例3求下列各式中的x的值32log)1(64x68log)2(xx100lg)3(xe2ln)4(例题分析3、运用指数运算求值讲授新课4.对数的性质（1）负数和零没有对数（∵在指数式中N>0）（2）01loga（3）1aalog即：1的对数是0即：底数的对数是1（4）对数恒等式：logaNaN（5）对数恒等式：lognaan．(0,1)aa且性质：巩固练习221012(,)logbabbabBbaa2ab、指数式且相应的对数式是（）AlogClogb=2DlogD2、对数式2(21)log1xx中x的取值范围是______}121|{xx3.3.求下列各式的值求下列各式的值161log161（1）（2）5log51（3）（4）11000lg3ln10巩固练习1、对数的定义2、指数式和对数式的互换；一般地,ax=N(a>0,a≠1),那么数x叫做以a为底N的对数,记作logaN=x。(式中的a叫做对数的底数,N叫做真数.)归纳小结NaxNxalog(0,1)aa且归纳小结（1）负数和零没有对数（2）01loga（3）1aalog即：1的对数是0即：底数的对数是14、对数的性质(0,1)aa且3、运用指数运算求值布置作业作业：P74习题A组1、2