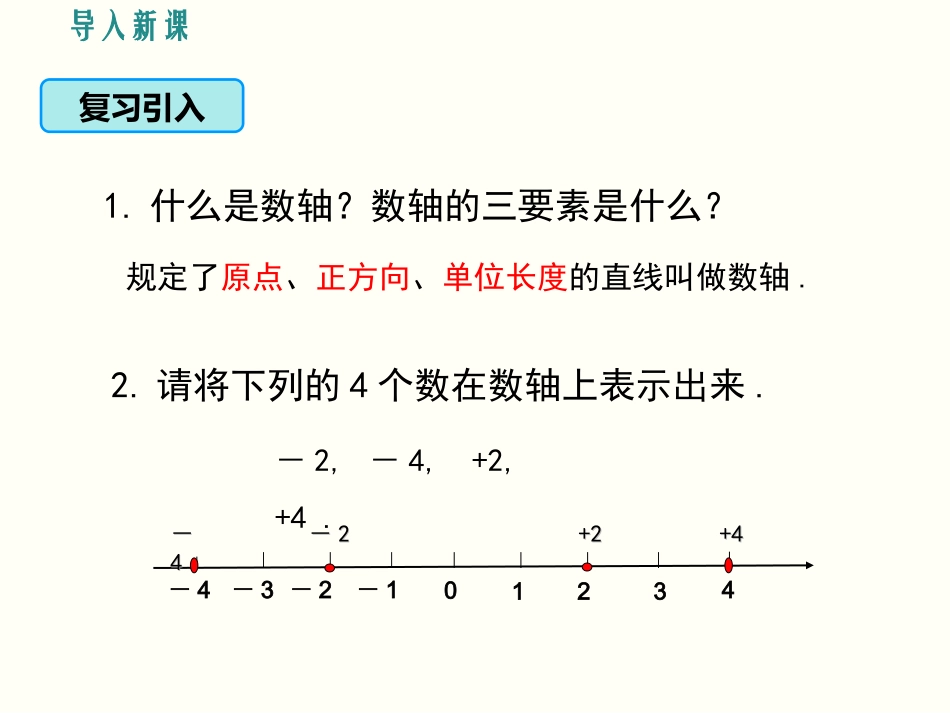
1.2数轴、相反数和绝对值第1章有理数第2课时相反数导入新课复习引入规定了原点、正方向、单位长度的直线叫做数轴.2.请将下列的4个数在数轴上表示出来.1.什么是数轴?数轴的三要素是什么?-2,-4,+2,+4.0-4-3-2-12134--44+4+4+2+2--22讲授新课相反数的意义一问题1:-2和+2,-4和+4各有什么相同点和不同点?22数字相同符号不同问题引入像-2和2,4和-4这样,只有符号不同的两个数互为相反数.概念归纳特别规定:0的相反数是0.一般地,数a的相反数是-a,这里a表示任意一个数,即它可以是正数、负数或者0.问题2:-2和+2,-4和+4在数轴上的位置有什么关系?在数轴上,-2与+2,-4和+4所对应的点位于原点两侧,且与原点的距离相等.想一想数轴上表示相反数的两个点和原点有什么关系?2.互为相反数的两个数到原点的距离相等.1.互为相反数的两个数分别位于原点的两侧(0除外);0-4-3-2-12134--44+4+4+2+2--22思考数轴上与原点距离是2的点有____个,这些点表示的数是________;与原点的距离是4的点有____个,这些点表示的数是________.02-2两2和-24和-4两一般地,设a是一个正数,数轴上与原点的距离是a的点有_____个,它们分别在原点的___________,表示_________,我们说这两点关于原点________,这两个数是一对__________.注意:a和–a到原点的距离相等.两左右两侧-a和a对称归纳相反数典例精析例1写出下列各数的相反数:解:3的相反数是-3;-7的相反数是7;-2.1的相反数是2.1;0的相反数是0;20的相反数是-20;的相反数是-;3232115的相反数是.115115-20,0321.2-7-3,,,,,思考:如何求数a的相反数呢?a的相反数是-a,a可表示任意有理数.在一个数前面加上“-”号表示求这个数的相反数,如果在这些数前面加上“+”号呢?在一个数前面加上“+”仍表示这个数,“+”号可省略.化简下列各数:(1)-(+10);(2)+(-0.15);(3)+(+3);(4)-(-12);(5)+[-(-1.1)];(6)-[+(-7)].例2解:(1)-(+10)=-10;(2)+(-0.15)=-0.15;(3)+(+3)=3;(4)-(-12)=12;(5)+[-(-1.1)]=+(+1.1)=1.1;(6)-[+(-7)]=-(-7)=7.由内向外依次去括号1.下列几对数中互为相反数的一对为().A与B.与C.与D.8与-(-8))8()8()8()8()8()8(C当堂练习2.判断(1)任何数都有相反数()(2)-5是相反数()(3)一定是负数()(4)与互为相反数()(5)-(-5)的相反数是5()(6)符号不同的两个数互为相反数()a-31-3√×××××课堂小结相反数定义应用只有符号不同的两个数互为相反数;0的相反数是0代数意义几何意义数a的相反数是-a两个互为相反数的数在数轴上所表示的点在原点的两旁,且与原点的距离相等求某数的相反数进行化简:-(-a)=a对于数字前面含有多个符号的数的化简,应如何简单有效的进行?归纳思考若2前面有2000个正号,化简后的结果是.若2前面有2001个负号,化简后的结果是.作业布置课本第10页练习1,2,3