一元二次方程知识体系构建VIP免费

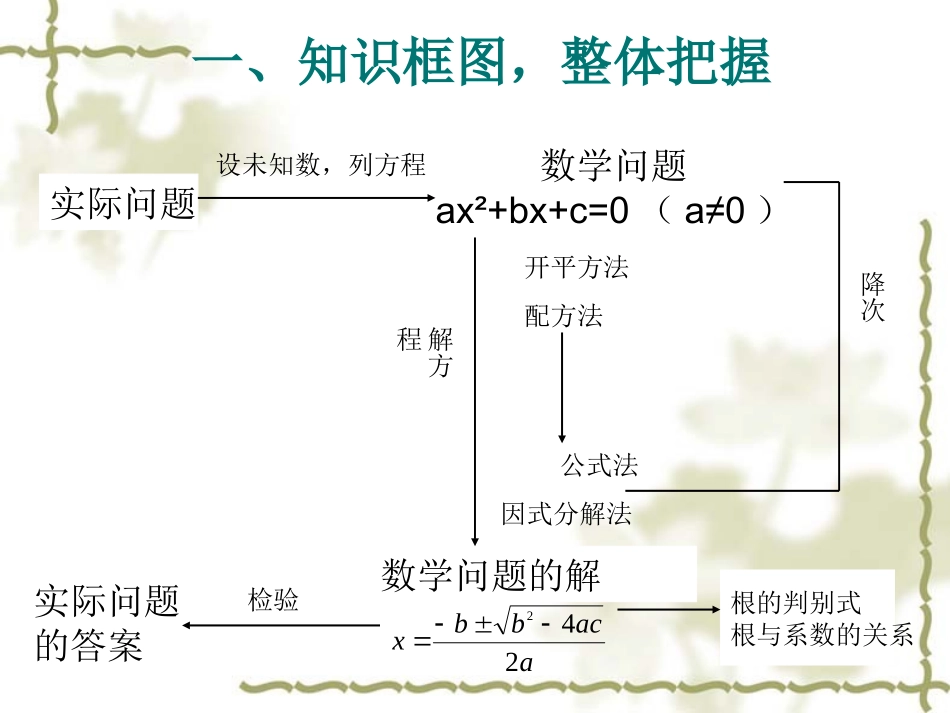
一、知识框图，整体把握实际问题数学问题ax²+bx+c=0（a≠0）实际问题的答案数学问题的解根的判别式根与系数的关系设未知数，列方程解方程开平方法配方法公式法因式分解法降次检验aacbbx242二、释疑解惑，加深理解1.一元二次方程的一般形式为ax²+bx+c=0（a，b，c为常数，且a≠0），这里二次项系数a≠0这一点往往在解题过程中易忽视，而致结论出错。m=2思考：若关于x的一元二次方程（m-1）x²+5x+m²-3m+2=0有一根为0，则常数m的值为。对于具体的方程，一定要认真观察，分析方程的特征，选择恰当的方法予以求解。无论选择哪种方法来求解方程，降次思想是它的基本思想。2.一元二次方程的解法开平方法、配方法、公式法和因式分解法（1）根的判别式Δ=b²-4ac与0的大小关系可直接确定方程的根的情况:当Δ=b²-4ac＞0时，方程有两个不相等的实数根；当Δ=b²-4ac=0时，方程有两个相等的实数根；当Δ=b²-4ac＜0时，方程没有实数根。ab3.根的判别式及根与系数的关系（2）根与系数的关系：若方程ax²+bx+c=0（a≠0）的两个实数根为x1，x2，则x1+x2=，x1.x2=。ac4.列一元二次方程解实际问题是数学应用的具体体现，如解决传播类问题、增长（降低）率问题、利润问题及几何图形的计算问题等，而解决这些实际问题的关键是弄清题意，找到其中的等量关系，恰当设未知数，建立方程并予以求解。需注意的是，应根据问题的实际意义检验结果是否合理。三、典例精析，复习新知例1已知关于x的一元二次方程：（m+n-1）x（m+n）²+1-（m+n）x+mn=0，则m+n的值为。-1例2已知a是方程x²-2014x+1=0的一个根，求代数式的值12014201322aaa解：根据方程根的定义，有a²-2014a+1=0，从而a²-2013a=a-1，a²+1=2014a，故原式。201320141112aaaaaaaa例3已知关于x的方程：x²-2（m+1）x+m²=0有两个实数根，试求m的最小整数值。解：由题意，有Δ=[-2（m+1）]²-4×1×m²=8m+4≥0，∴m≥,故m的最小整数值为0。21例4已知关于x的方程x²-2x-a=0。（1）若方程有两个不相等的实数根，求a的取值范围；解：可直接由Δ=b²-4ac=4+4a＞0，得a＞-1。解：不妨先令。从而有解得a=-3，而当a=-3时，原方程没有实数根，故的值不能等于。32321121xx。322.2121axxxx（2）若此方程的两个实数根为x1，x2，则的值能等于吗？如果能，请求出a的值；如果不能，请说明理由。2111xx322111xx例5某零售商购进一批单价为16元的玩具，销售一段时间后，为了获得更多的利润，商店决定提高销售价格，经试验发现，若按每件20元销售时，每月可销售360件；若按每件25元销售时，每月能卖出210件，假定每月销售件数y（件）是价格x的一次函数。（1）试求y与x之间的关系式；（2）当销售价定为多少时，每月获得1800元利润？（3）每月的利润能达到2000元吗？为什么？解:（1）设y=kx+b，把（20,360），（25,210）代入，可得y=-30x+960（16≤x≤32）。（2）设获利为w元，则由题意，得w=（x-16）（-30x+960）。当w=1800时，有（x-16）（-30x+960）=1800，解得x1=22，x2=26。故销售价定在22元或26元时，每月可获得1800元利润。（3）令（x-16）（-30x+960）=2000，整理，得3x²-144x+1736=0。此时Δ=b²-4ac=（-144）²-4×3×1736=-96＜0。所以原方程无解，即每月利润不能为2000元。四、复习训练，巩固提高1.若方程（m²-2）x²-1=0有一根为1，则m的值是（）。±42.若方程3x²-5x-2=0有一根为a，则6a²-10a的值是（）。33.已知关于x的方程：（a-2）x²-2（a-1）x+（a+1）=0，a为非负数时，求下列各a的取值。（1）方程只有一个实数根？（2）方程有两个相等实数根？（3）方程有两个不等实数根？a=2a=3a=0或a=14.百货商店服装柜在销售中发现：某品牌童装平均每天可售出20件，每件盈利40元，为了迎接”六一“国际儿童节，商店决定采取适当的降价措施，扩大销售量，增加盈利，尽量减少库存。经市场调查发现：如果每件童装降价1元，那么平均每天可多售出2件，想要平均每天销售这种童装盈利1200元，在对顾客利益最大的基础上，童装应降价多少元？解：设每件童装应降价x元，由题意，列方程为（40-x）(20+2x)=1200，解得x1=20，x2=10。因为要对顾客利益最大，所以每件童装应降价20元。五、师生互动，课堂小结通过本节课的学习，对本章的知识你有哪些新的认识和体会？与同伴进行交流。课后作业布置作业：从教材“复习题21”中选取。