最新北师大版九年级上课件-成比例线段VIP免费

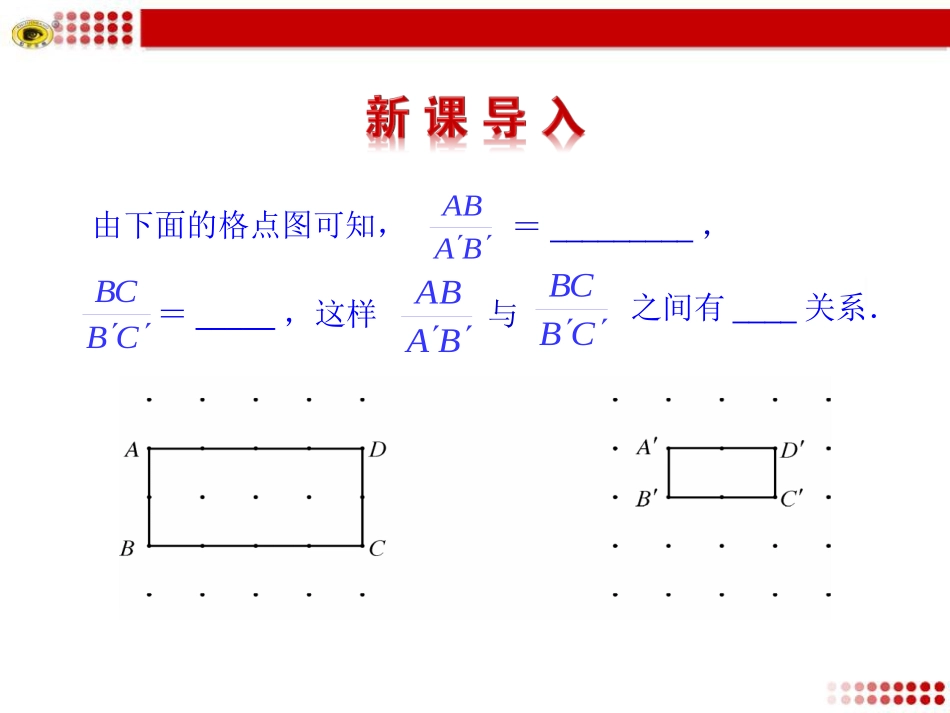
第四章图形的相似1成比例线段1.理解成比例线段的概念，能判断四条线段是否成比例.2.理解比例的基本性质．3.能应用比例的基本性质解决问题.BAABCBBCBAABCBBC由下面的格点图可知，＝_________，＝_____，这样与之间有____关系．四条线段a,b,c,d中，如果a与b的比等于c与d的比，那么，这四条线段a,b,c,d叫做成比例线段，简称比例线段．此时也称这四条线段成比例．ac,bd即定义【例1】判断下列线段a，b，c，d是否是成比例线段：（1）a＝4，b＝6，c＝5，d＝10.【解析】∵∴线段a，b，c，d不是成比例线段．4263ab，51102cd，acbd∴，【例题】515235（2）a＝2，b＝，c＝，d＝．22555ab，21525553cd，【解析】∵acbd，∴∴线段a，b，c，d是成比例线段．对于成比例线段我们有下面的结论：dcbadcba如果，那么ad＝bc．如果ad＝bc（a，b，c，d都不等于0），那么．判断下列线段是否是成比例线段：（1）a＝2cm，b＝4cm，c＝3m，d＝6m.（2）a＝0.8，b＝3，c＝1，d＝2.4．【解析】（1）∵a:b=c:d，∴a,b,c,d是成比例线段；（2）∵a:c=d:b,∴a,c,d,b是成比例线段.【跟踪训练】acbd，abcd.bd【例2】证明：（1）若那么acbd，证明：∵在等式两边同加上1，abcd.bd∴ac11bd，∴【例题】acbdacabcdabcd（，）.（2）如果，那么acbd，ac.abcd证明：∵∴ad＝bc，在等式两边同加上ac，∴ad＋ac＝bc＋ac，∴ac－ad＝ac－bc，∴a（c－d）＝（a－b）c，两边同除以（a－b）（c－d），∴23babbabaa，那么，各等于多少？2．已知cbba1．已知：线段a,b,c满足关系式且b＝4，那么ac＝______．，16答案：352【跟踪训练】比例的基本性质如果a:b=c:d，那么ad=bc.因为a:b=c:d，即比例的内项乘积等于外项乘积.两边同乘以bd，得ad=bc.上述性质反过来也对，就是如果ad=bc(a,b,c,d都不等于0)，那么a:b=c:d.dcba比例的基本性质a︰b=c︰dad=bc.特殊地说：a︰b=b︰cb2=ac.综合地说：如果那么PA·PD=PB·PC；如果那么AD·CD=EB·DF；如果HF·NF=HE·NK,那么PAPCPBPD，CDDFEBAD，HFNK；NFHE如果EF·BD=AC·EA,那么EFACBD.EA【跟踪训练】说明：(1)一个等积式可以改写成八个比例式(一般情况下比值各不相同)；(2)对调比例式的内项或外项，比例式仍然成立(比值变了).bdcabcdacabddabcadcbdbacacdbcbad合比性质1acbd如果，等式两边同时加上，得即,ddcbba(0)acabcdbdbdbd如果，那么，等比性质312n123123n123n1n123n1aaaabbbbbbbaaaaab0,.bbbbb如果，且那么你能证明吗？【例3】已知：在三角形ABC中，ADAEDBEC，ABCDE求证：ABAC(1).DBECADAE(2).ABAC证明（1）ADAEDBEC，ADDBAEECDBEC，ABAC.DBEC（2）ADAEDBEC，DBECADAE，DBADECAEADAE，ABACADAE，ADAEABAC.【例题】1.如图，ＤＥ是△ＡＢＣ的中位线，请尽可能多的写出比例线段.EDCBＡ【解析】ADAEDEADAE..ABACBCDBEC（1）=（2）【跟踪训练】xy5x2.,.3y4y已知求xy5,3y4xy15y4154411.4xyyyxy【解析】，，1.（德化·中考）下列各组线段（单位：㎝）中，成比例线段的是（）A．1，2，3，4B．1，2，2，4C．3，5，9，13D．1，2，2，3B2.已知a:b:c=2:5:6，求的值.【解析】由题意得c2b-3ac-5b2aabck256，则a=2k,b=5k,c=6k，2a5b-c4k25k6k23.3a-2bc6k10k6k2我们总是梦想着天边的一座奇妙的玫瑰园，却不去欣赏今天就开在我们窗口的玫瑰．——佚名