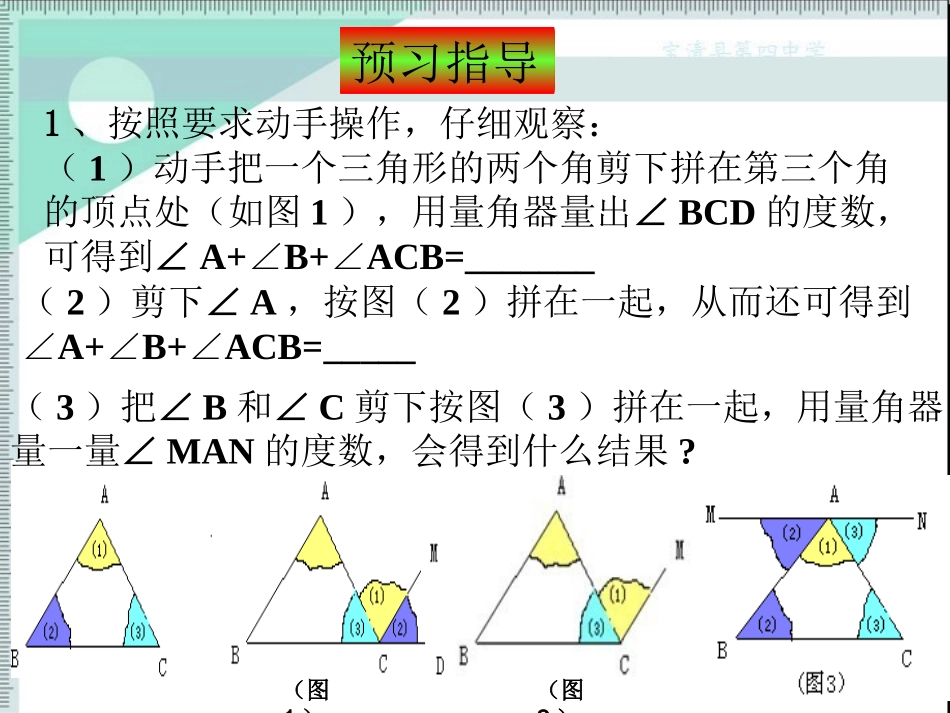
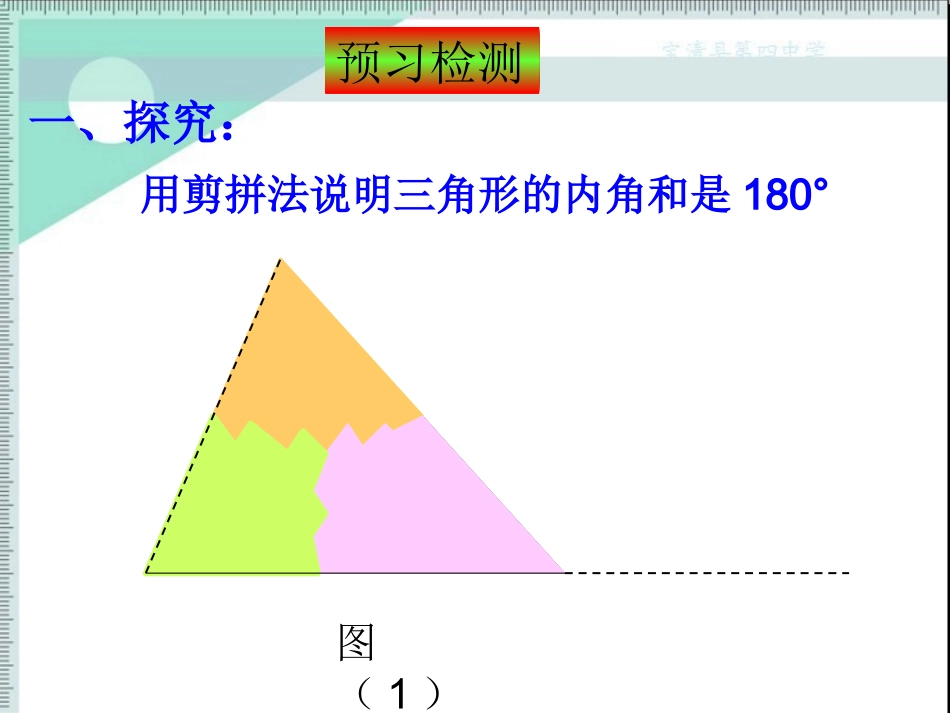
•三角形的内角和1、按照要求动手操作,仔细观察:(1)动手把一个三角形的两个角剪下拼在第三个角的顶点处(如图1),用量角器量出∠BCD的度数,可得到∠A+B+ACB=∠∠_______(2)剪下∠A,按图(2)拼在一起,从而还可得到∠A+B+ACB=∠∠_____(3)把∠B和∠C剪下按图(3)拼在一起,用量角器量一量∠MAN的度数,会得到什么结果?(图1)(图2)预习指导用剪拼法说明三角形的内角和是180°一、探究:图(1)预习检测图(2)三角形的三个内角和等于180°通过观察、操作得出结论:剪拼法巧妙的运用了转化的数学思想图(3)温馨提示:三角形的内角和等于1800.命题:它是真命题吗?一个命题是否正确,需要经过使人信服的推理论证才能得出结论.而证明是由命题的题设(已知)出发,经过严密的推理,最后推出结论(求证)正确的过程.形状不同的三角形有无数个,我们不可能通过上面的办法一一验证.再加上其验证过程中存在误差,不能保证其有效性.所以我们需要一种能证明任意一个三角形的内角和等于180°的方法.这个方法就是—证明.1、证明几何命题的步骤:(1)根据题意,画出图形;(2)根据题设、结论、结合图形,写出已知、求证;(3)写出证明过程。为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。在证明过程开始时,需要添加的辅助线要先写清楚。2、辅助线二、探究:用平行线法证明三角形的内角和等于1800已知:如图,△ABC求证:∠A+∠B+C=180°∠BCA根据剪拼法的启示,你有几种证明方法?过C作CEBA∥,∴∠A=1∠(两直线平行,内错角相等)∠B=2∠又∵∠1+2+ACB=180°∠∠∴∠A+B+ACB=180°∠∠??(两直线平行,同位角相等)??(等量代换)证明:作BC的延长线CD,ABC)E1)(平角的定义)2D已知:如图,△ABC求证:∠A+∠B+C=180°∠ABC)E1ABC)E1)2D图(2)图(3)另两种方法的几何图形你还有其他方法来证明三角形内角和等于1800吗?添加辅助线思路:1、构造平角ABCE图1EABCDF图2(ABCEDF((1234(图32、构造同旁内角开启智慧ABC演示123折纸法三角形的内角和等于1800.三角形内角和定理:通过推理、归纳、探索得出温馨提示:证明三角形内角和定理方法很多,基本思想是利用平行线性质、平角定义证明自我检测(1)在△ABC中,∠A=30°,∠B=50°,则∠C=____。(2)在△ABC中,∠C=90°,∠B=50°,则∠A=____。(3)在△ABC中,A=40°∠,∠A=2B∠,则∠C=____。100°40°120°32三、新知应用例:已知:在△ABC中,∠C=ABC=2A∠∠,BD是AC边上的高,求∠DBC的度数。∴X+2X+2X=180(三角形内角和定理)。解得X=36。∴∠C=72°在△ABC中∵∠BDC=90°∴∠DBC=180°-90°-72°(三角形内角和定理)∴∠DBC=18°ABCD解:设∠A=X°则∠C=ABC=2X°∠一块模板如图所示,按规定AF、DE的延长线相交成700的角,但交点不在模板上,不便测量,于是,张师傅连接AD,测得∠FAD=360,∠ADE=740,请问根据这两个角度如何判断模板是否合格?ABCDEFO四、拓展提升这节课你有哪些收获呢?五、收获与感悟1、如果三角形的三个内角的度数比是2:3:4,则它是()A.锐角三角形B.钝角三角形;C.直角三角形D.钝角或直角三角形2、下列说法正确的是()A.三角形的内角中最多有一个锐角;B.三角形的内角中最多有两个锐角C.三角形的内角中最多有一个直角;D.三角形的内角都大于60°3、已知△ABC中,A=2(B+C),∠∠∠则∠A的度数为()A.100°B.120°C.140°D.160°ACB当堂检测21DCBA4、如图所示,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数为________.5、如图△ABC中,CD平分∠ACB,DEBC,∥∠A=70°∠B=50°,求∠BDC的度数。80°∠BDC=100°作业课本76页第一题的1,2,3小题第三题