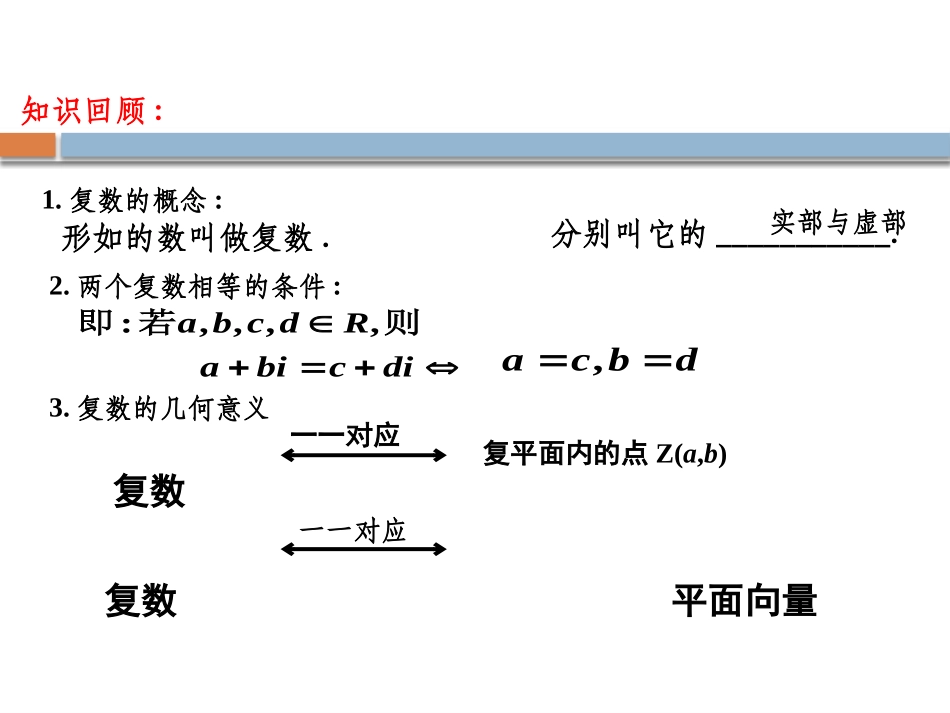
3.2.1复数代数形式的加减运算及几何意义-----韦应俭[学习目标]1、掌握复数的加法与减法的加减法运算法则。2、理解复数的加法与减法的几何意义,能够运用“数形结合”的思想解题。知识回顾:1.复数的概念:形如的数叫做复数.分别叫它的___________.实部与虚部dicbiaRdcba则若即,,,,:dbca,2.两个复数相等的条件:复数复平面内的点Z(a,b)一一对应复数平面向量一一对应3.复数的几何意义1、复数的加法法则:设是任意两个复数,那么它们的和:(𝒂+𝒃𝒊¿+(𝒄+𝒅𝒊)=(𝒂+𝒄)+(𝒃+𝒅)𝒊点评:(1)复数的加法运算法则是一种规定。当时与实数加法法则保持一致(2)很明显,两个复数的和仍然是一个复数。对于复数的加法可以推广到多个复数相加的情形。思考:类比实数的运算法则能否得到复数的运算法则?证:设,Z2=,Z3=(则Z1+Z2=()+(),Z2+Z1=显然同理可得点评:实数加法运算的交换律、结合律在复数集C中依然成立。探究?复数的加法满足交换律,结合律吗?Z1+Z2=Z2+Z1(Z1+Z2)+Z3=Z1+(Z2+Z3)复数的加法满足交换律、结合律,即对任意),(2dcZ),(1baZZxO设及分别与复数及复数对应,则∴向量就是与复数对应的向量.探究?复数与复平面内的向量有一一的对应关系。我们讨论过向量加法的几何意义,你能由此出发讨论复数加法的几何意义吗?==()思维的提升思考?复数的减法规定是加法的逆运算,即把满足()+()=的复数叫做复数减去复数的差,记作()-()请同学们推导复数的减法法则。事实上,由复数相等的定义,有:𝒄+𝒙=𝒂,𝒅+𝒚=𝒃由此,所以即:点评:根据复数相等的定义,我们可以得出复数的减法法则,且知两个复数的差是唯一确定的复数。复数是否有减法?如何理解复数的减法?深入探究yxO1Z2Z复数减法的几何意义:-=复数的加法几何意义同构于向量加法几何意义。复数减法的几何意义同构于向量减法的几何意义。注意“同构”一词。深入探究?类比复数加法的几何意义,请指出复数减法的几何意义?讲解例题例1计算(56)(2)(34)iii-+---+(56)(2)(34)(523)(614)11iiiii-+---+=--+---=-解:例2在复平面内,复数与对应的向量分别是与,其中O是原点,求向量,对应的复数.学以致用1(2+4i)+(3-4i)2.5-(3+2i)3.(-3-4i)+(2+i)-(1-5i)4.(2-i)-(2+3i)+4i=(2+3)+(4-4)i=5=(5-3)+(0-2)i=2-2i=(-3+2-1)+(-4+1+5)i=-2+2i=(2-2+0)+(-1-3+4)i=05.(3+5i)+(3-4i)6.(-3+2i)-(4-5i)7.(5-6i)+(-2-2i)-(3+3i)=(3+3)+(5-4)i=6+i=(-3-4)+[2-(-5)]i=-7+7i=(5-2-3)+(-6-2-3)i=-11i巩固提高8.设(),且,求解:∵∴∴𝟑+𝒙=𝟓,𝟐−𝒚=−𝟔.∴𝒙=𝟐𝒚=𝟖∴三、课堂练习1、计算:(1)(-3-4i)+(2+i)-(1-5i)=_____(2)(3-2i)-(2+i)-(________)=1+6i2、已知为纯虚数,且则=_______=_______3、已知复数,试求对应的点关于虚轴对称点的复数。-𝟐+𝟐𝒊--23𝟒𝒊4、复平面内关于原点对称的两点对应的复数为且满足,求和。-𝟐-𝒊1.复数的加、减运算法则表明,若干个复数的代数和仍是一个复数,复数的和差运算可转化为复数的实部、虚部的和差运算.2.在几何背景下求点或向量对应的复数,即求点或向量的坐标,有关复数模的问题,根据其几何意义,有时可转化为距离问题处理.3.由于复数能用向量表示,从而使得复数的加、减运算与向量的加、减运算在算理上完全一致,给复数的加、减运算赋予了几何意义.在实际应用中,既可以将复数的运算转化为向量运算,也可以将向量的运算转化为复数运算,二者对立统一.小结作业