反比例函数复习有关面积复习课件tVIP免费

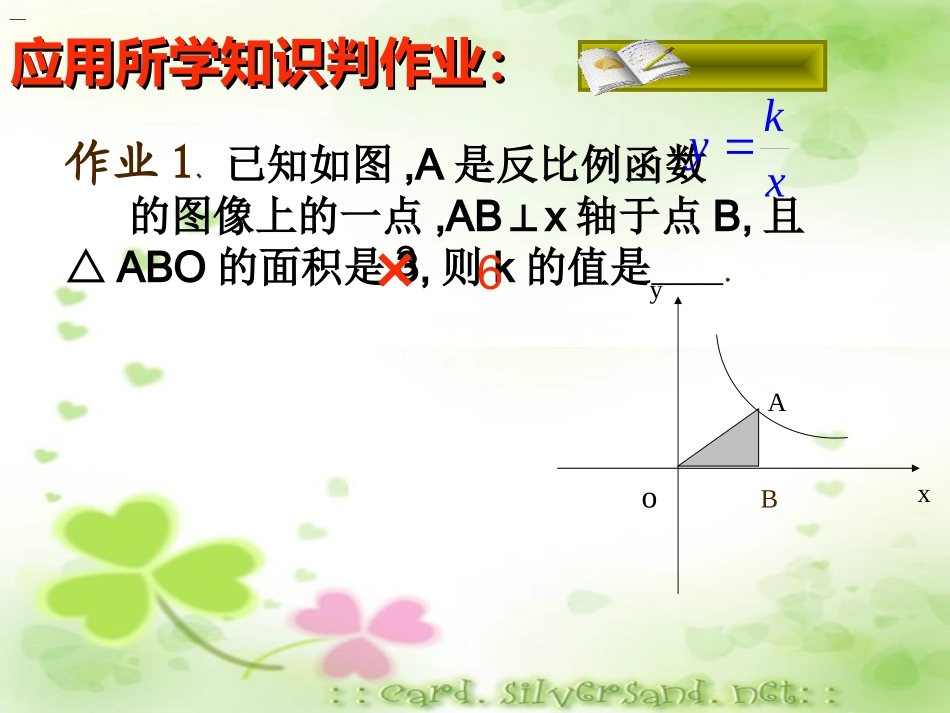
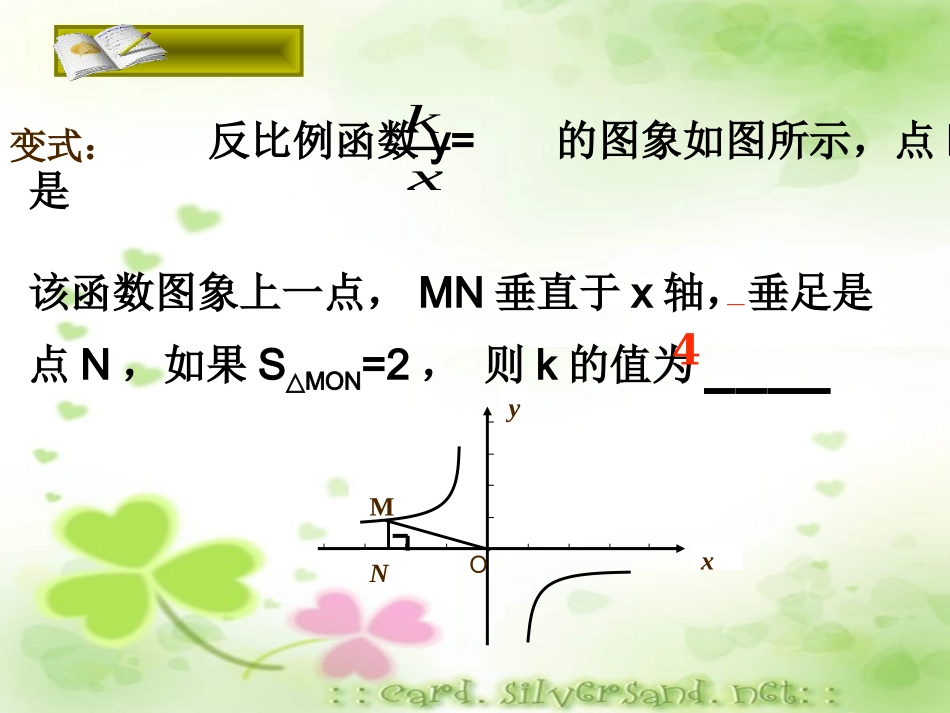
凤台四中王辉2013.4应用所学知识判作业：应用所学知识判作业：作业1﹑已知如图,A是反比例函数的图像上的一点,ABx⊥轴于点B,且△ABO的面积是3,则k的值是＿＿＿．yoABxxky3×6xk反比例函数y=的图象如图所示，点M是该函数图象上一点，MN垂直于x轴，垂足是点N，如果SMON△=2，则k的值为____NMxyO－4变式：作业2、如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,垂足为M、N,若S四边形PMON为3,则这个反比例函数的关系式是____xyoMNp应用所学知识判作业：应用所学知识判作业：作业3、如图，直线y=mx与双曲线y=交于A、B两点，过点A作AMx⊥轴，垂足为M，连结BM,若=2，则k的值是（C）A．2B、m-2C、mD、4OxkABMS解∵直线y=mx与双曲线y=交于A、B两点关于原点O对称∴=2SAOM△=k=2∴k=2。ABMSxk×A作业4、直线y=kx（k＞0）与双曲线交于A（x1，y1），B（x2，y2）两点，则2x1y2－7x2y1的值等于＿＿＿．xy6解：由题意知，直线y=kx（k＞0）过原点和一、三象限，且与双曲线交于两点，则这两点关于原点对称，∴x1=-x2，y1=-y2，又∵点A点B在双曲线上，∴x1y1=6，x2y2=6，∵由反比例函数的性质可知，A、B两点关于原点对称，∴x1y2=-6，x2y1=-6，∴2x1y2-7x2y1=2×（-6）-7×（-6）=30．故答案为：30．30变式：直线y=k1x与双曲线交于A（x1，y1），B（x2，y2）两点，若2x1y2－7x2y1=－30，则k2=.2kyx－61、已知：A是双曲线上的一点，过点A向x轴作垂线，垂足为B，△AOB的面积是4,则它的解析式为xyxy88或2、如图，A是反比例函数图象上一点，过点A作ABy⊥轴于点B，点P的坐标为（－1,0），△ABP面积为2，则这个反比例函数的解析式为.3﹑如图，点AB﹑是双曲线上的点，分别经过AB﹑两点向轴、轴作垂线段，若则＿＿O3yxxy1S阴影，12SSxyABOS1S244、如图，点A在双曲线上，点B在双曲线上，且AB∥x轴，C、D在x轴上，若四边形ABCD为矩形，则它的面积为.3yxO2变式：如图,反比例函数和（）在第一象限的图象，直线AB//x轴，并分别交两条曲线于A、B两点，若S△AOB=2，则的值（）A.1B.2C.4D.81kyx2kyx12kk21kk通过本堂课的学习，你有什么收获吗？1、S△=2、反比例图形关于原点成中心对称3、根据面积求k值要注意图象的象限、K值的符号.4、在反比例函数的图象组合图形的面积计算要注意选择恰当的分解方法.5、各种数学思想理解：转化思想、分类讨论、数形结合思想、方程思想、整体思想…….kS矩形k21思索归纳基础训练P46探究创新1、如图,过y轴正半轴上的任意一点P，作x轴的平行线，分别与两反比例函数的图象交于点A和点B，若点C是x轴上任意一点，连接AC、BC，则△ABC的面积为（）A．3B．4C．5D．62、如图，双曲线(k＞0)经过矩形OABC的边BC的中点E，交AB于点D。若梯形ODBC的面积为3，则双曲线的解析式为()．(A)(B)(C)(D)xkyxy1xy2xy3xy61、若反比例函数与正比例函数y＝2x的图象没有交点，则k的取值范围是______；2、若反比例函数与一次函数y＝kx＋2的图象有交点，则k的取值范围是______．Oxky1xkyk＜－1k≠0变式：若反比例函数y=与一次函数y＝－x＋2的图象有交点，则k的取值范围是.．Oxk