解直角三角形(1)课件VIP免费

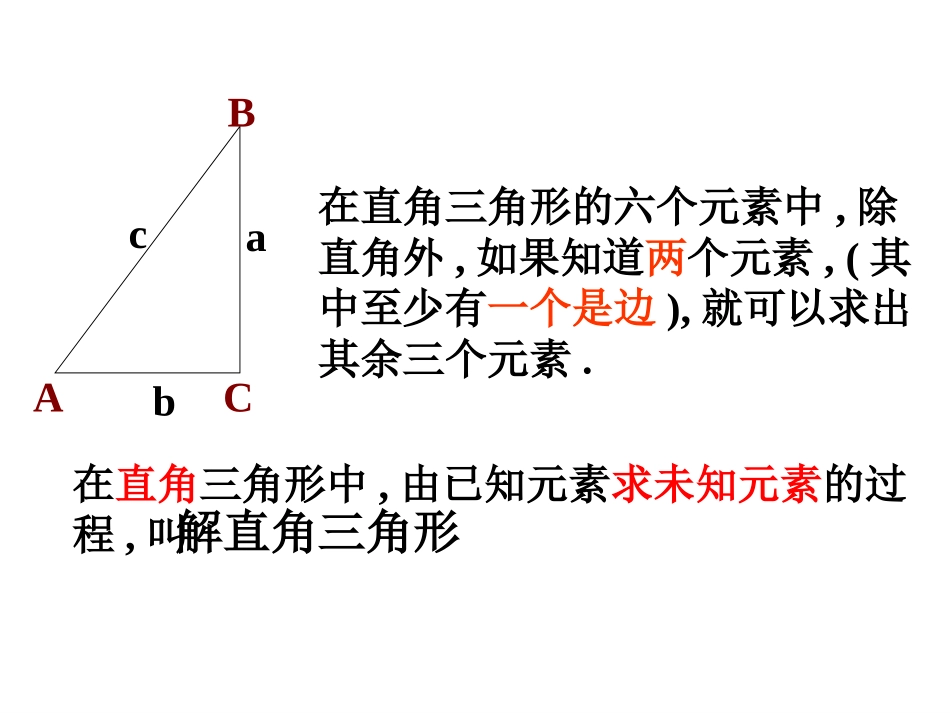
（2）两锐角之间的关系∠A＋∠B＝90°（3）边角之间的关系caAA斜边的对边sincbBB斜边的对边sincbAA斜边的邻边coscaBB斜边的邻边cosbaAAA的邻边的对边tanabBBB的邻边的对边tan（1）三边之间的关系222cba（勾股定理）ABabcC三角形有六个元素,分别是______和______.ＡＣＢ三条边三个角在RtABC△中,C=90°∠(1)根据∠A=45°,斜边AB=12,你能求出这个三角形的其他元素吗?(2)根据AC=,斜边AB=6,你能求出这个三角形的其他元素吗?(3)根据∠A=60°,B=30°,∠你能求出这个三角形的其他元素吗?33在直角三角形的六个元素中,除直角外,如果知道两个元素,(其中至少有一个是边),就可以求出其余三个元素.在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形ACBabc解直角三角形(1)解直角三角形(1)知道是求什么吗?解:326tanACBCA060A000306090B22AC2AB.,6BC,2AC,90C,ABCRt.1解直角三角形中在例ACB26知道是求什么吗?例2.在RtABC△中,C=90°,B=35°b=20,∠∠解这个直角三角形.(精确到0.1)70.035tan057.035sin0解:cbBtan35tan20Btanba6.2870.020cbBsin35sin20Bsinbc1.3557.020BCA35°20在RtABC△中,C=90°,∠根据下列条件解直角三角形.(1)a=30,b=20(2)B=72°,c=14∠要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.现有一个长6m的梯子.问:(1)使用这个梯子最高可以安全攀上多高的平房?(精确到0.1m)这个问题归结为:在RtABC△中,已知∠A=75°,斜边AB=6,求BC的长角α越大,攀上的高度就越高.ACB要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α一般要满足50°≤α≤75°.现有一个长6m的梯子.问:(2)当梯子底端距离墙面2.4m时,梯子与地面所成的角α等于多少(精确到1°)?这时人能否安全使用这个梯子?这个问题归结为:在RtABC△中,已知AC=2.4m,斜边AB=6,,求锐角α的度数?ACB角α是否在50°≤α≤75°请你谈谈对本节学习内容的体会和感受。今天你有什么收获?在遇到解直角三形的问题时，最好先画一个直角三角形的草图，按题意标明哪些元素是已知的，哪些元素是未知的。以得于分析解决问题选取关系式时要尽量利用原始数据，以防止“累积错误”解直角三角形的方法遵循“有斜用弦，无斜用切；宁乘勿除，化斜为直”（2）两锐角之间的关系∠A＋∠B＝90°（3）边角之间的关系caAA斜边的对边sincbBB斜边的对边sincbAA斜边的邻边coscaBB斜边的邻边cosbaAAA的邻边的对边tanabBBB的邻边的对边tan（1）三边之间的关系222cba（勾股定理）ABabcC解直角三角形的重要依据已知斜边求直边，已知直边求直边，已知两边求一边，已知两边求一角，已知锐角求锐角，已知直边求斜边，计算方法要选择，正弦余弦很方便；正切余切理当然；函数关系要选好；勾股定理最方便；互余关系要记好；用除还需正余弦；能用乘法不用除.优选关系式1、课本P101中1题和2题2、预习下一节内容，要求了解什么是仰角和俯角补充作业：3如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.ABC4503004cm作业作业•悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.去总结下课了!结束寄语结束寄语比萨斜塔问题：设塔顶中心点为B，塔身中心线与垂直中心线的夹角为A，过B点向垂直中心线引垂线，垂足为点C（如图），在Rt△ABC中，∠C＝90°，BC＝5.2m，AB＝54.5m0954.05.542.5sinABBCA所以∠A≈5°28′2001年竣工，使塔顶中心点偏离垂直中心线的距离比纠偏前减少了43.8cm,你能求出纠偏后塔身中心线与垂直中心线的夹角吗？ABCABCP91例3：2008年10月15日“神舟”7号载人航天飞船发射成功．当飞船完成变轨后，就在离地球表面350km的圆形轨道上运行．如图，当飞船运行到地球表面上P点的正上方时，从飞船上最远能直接看到地球上的点在什么位置？这样的最远点与P点的距离是多少？（地球半径约为6400km，结果精确到0.1km）分析：从飞船上能最远直接看到的地球上的点，应是视线与地球相切时...