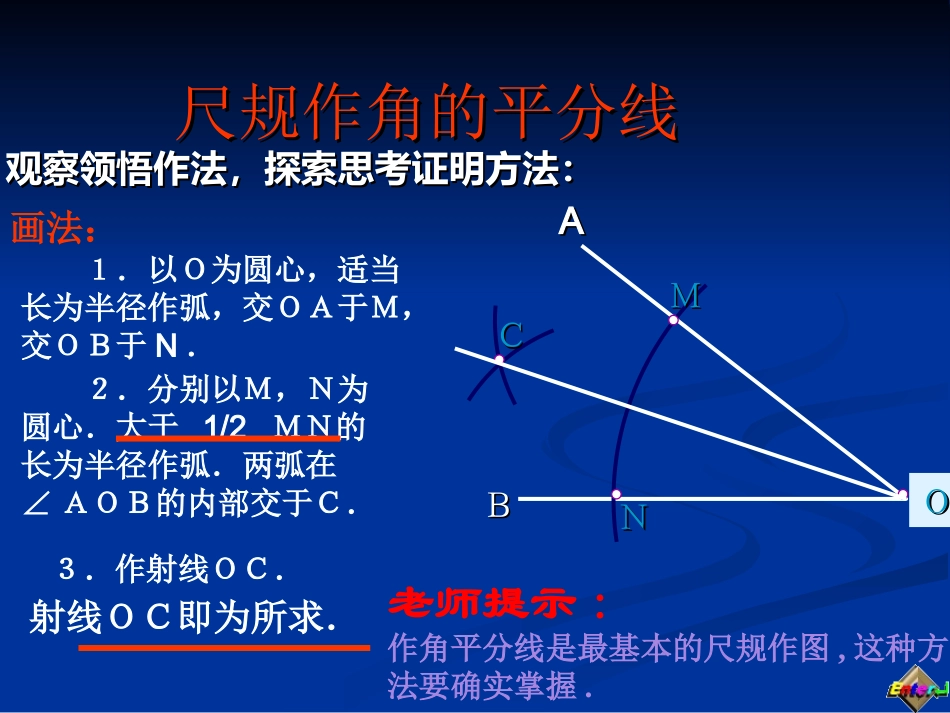
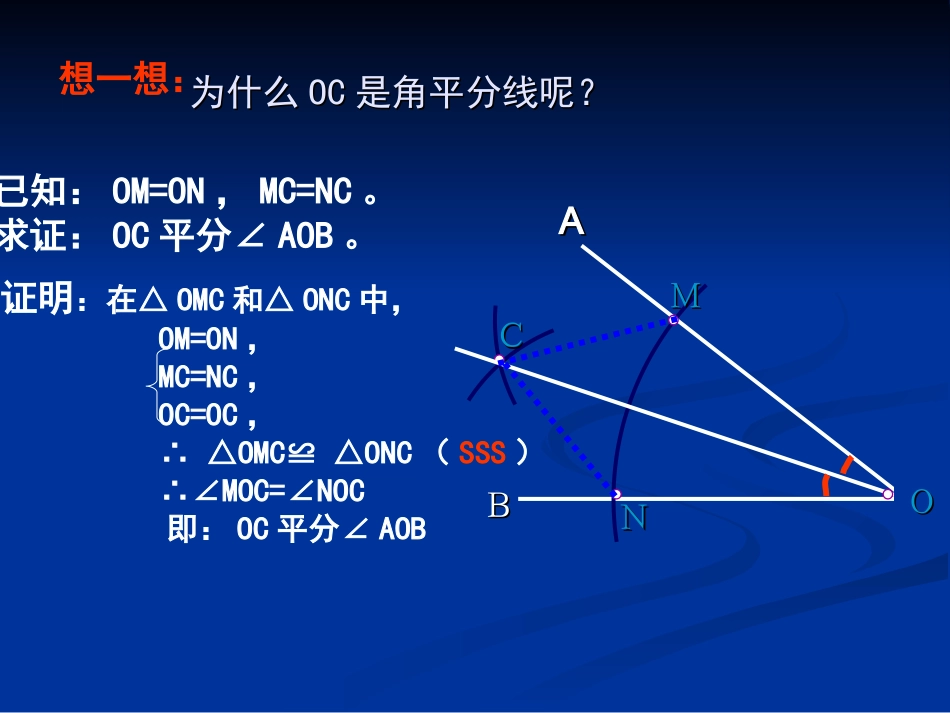
尺规作角的平分线尺规作角的平分线观察领悟作法,探索思考证明方法:观察领悟作法,探索思考证明方法:AABBOOMMNNCC画法:1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N.2.分别以M,N为圆心.大于1/2MN的长为半径作弧.两弧在∠AOB的内部交于C.3.作射线OC.射线OC即为所求.老师提示:作角平分线是最基本的尺规作图,这种方法要确实掌握.AABBMMNNCC为什么为什么OCOC是角平分线呢?是角平分线呢?OOO想一想:已知:OM=ON,MC=NC。求证:OC平分∠AOB。证明:在△OMC和△ONC中,OM=ON,MC=NC,OC=OC,∴△OMC≌△ONC(SSS)∴∠MOC=∠NOC即:OC平分∠AOB探索探索22将角将角AOBAOB对折对折,,再折出一个直角三角形再折出一个直角三角形((使第一使第一条折痕为斜边条折痕为斜边),),然后展开然后展开,,观察两次折叠形成观察两次折叠形成的三条折痕的三条折痕,,你能得到什么结论你能得到什么结论??OABAOBED操作测量题:OC是∠AOB的平分线,点P是射线OC上的任意一点,1.操作测量:取点P的三个不同的位置,分别过点P作PDOA⊥,PEOB,⊥点D、E为垂足,测量PD、PE的长.将三次数据填入下表:2.观察测量结果,猜想线段PD与PE的大小关系,写出结论:____________PDPE第一次第二次第三次COBAPD=PEpDE结论:在角平分线上的点到角的两边的距离相等题设:一个点在一个角的平分线上结论:它到角的两边的距离相等已知:OC是∠AOB的平分线,点P在OC上,PDOA⊥,PEOB⊥,垂足分别是D、E.求证:PD=PE.AOBPEDC已知:OC平分∠AOB,点P在OC上,PDOA⊥于D,PEOB⊥于E求证:PD=PEAOBEDPC例1:∵PD⊥OAPE⊥OB,证明:∴∠PDO=PEO=∠90°在△POD和Rt△PEO中∴△PDO≌△PEO(AAS)∠PDO=∠PEO∠AOC=∠BOCOP=OP∴PD=PE角平分线的性质:角的平分线上的点到角的两边的距离相等.到角的两边的距离相等的点在到角的两边的距离相等的点在角平分线上。角平分线上。结论:到角的两边的距离相等的点在角的平分线上。∵∵QD⊥OA,QE⊥OB,QD=QE.∴点Q在∠AOB的平分线上.角的平分线上的点到角的两边的距离相等.∵∵QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上∴QD=QE用数学语言表示为:思考:要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺1:20000)SO公路铁路例例22已知:如图,△已知:如图,△ABCABC的角平分线的角平分线BMBM、、CNCN相相交于点交于点P.P.求证:点求证:点PP到三边到三边ABAB、、BCBC、、CACA的距离相等的距离相等..证明:过点证明:过点PP作作PDPD、、PEPE、、PFPF分别分别垂直于垂直于ABAB、、BCBC、、CACA,垂足为,垂足为DD、、EE、、FF∵∵BMBM是是△△ABCABC的角平分线,点的角平分线,点PP在在BMBM上上∴∴PD=PEPD=PE((在角平分线上的点到角的两边的距离相等)在角平分线上的点到角的两边的距离相等)同理同理PE=PF.PE=PF.∴∴PD=PEPD=PE=PF.=PF.即点即点PP到边到边ABAB、、BCBC、、CACA的距离相等的距离相等DEFABCPMN练习:如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P.求证:点P到三边AB,BC,CA所在直线的距离相等.ABCDEPFGHBP1:画一个已知角的角平分线;及画一条已知直线的垂线;2:角平分线的性质:角的平分线上的点到角的两边的距离相等.3:角平分线的判定结论:到角的两边的距离相等的点在角平分线上。做一做已知:如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:EB=FC.老师期望:做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去.BAEDCF独立作业111.利用尺规作出三角形三个内角的平分线.老师期望:先分别作出不同形状的三角形,再按要求去作图.你发现了什么?