【精品课件】112余弦定理VIP免费

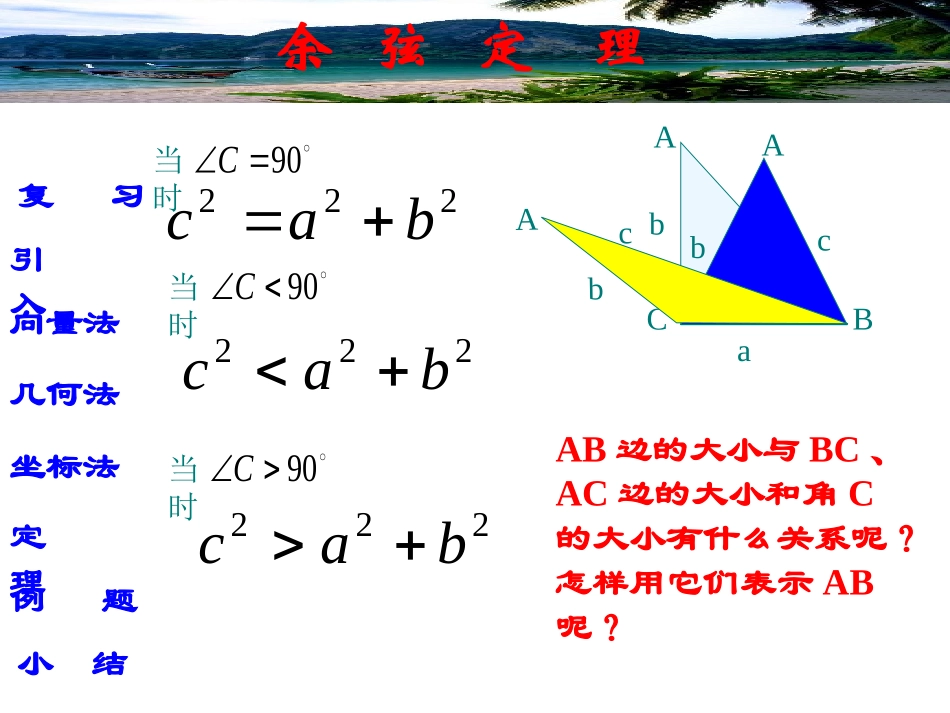
余弦定理1、向量的数量积：cosbaba2、勾股定理：AaBCbc222cba证明：CBACAB))((CBACCBACABABCBCBCBACACAC2222CBACAB复习引入向量法几何法坐标法例题定理小结AaBCbc余弦定理AcbAbc当时90C222bac当时90C222bac当时90C222bacAB边的大小与BC、AC边的大小和角C的大小有什么关系呢？怎样用它们表示AB呢？复习引入向量法几何法坐标法例题定理小结思考题：若ABC为任意三角形，已知角C，BC=a,CA=b,求AB边c.ABCabcCBACAB))((CBACCBACABABCBCBCBACACAC22)180cos(2220CBCCBACACAB解：Cabbaccos2222复习引入向量法几何法坐标法例题定理小结余弦定理定理：三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。Cabbaccos2222Abccbacos2222bcacbA2cos222abcbaC2cos222余弦定理可以解决以下两类有关三角形的问题：（1）已知三边求三个角；（2）已知两边和它们的夹角，求第三边和其他两个角。复习引入向量法几何法坐标法例题定理小结余弦定理ABCabcD当角C为锐角时证明：过A作ADCB交CB于D在Rt中ADCCACCDCACADcos,sin在中CACCBCBACCACCACCBCBCACCDCBCACBDADABcos2coscos2sin)()sin(222222222222Cabbaccos2222复习引入向量法几何法坐标法例题定理小结RtABD余弦定理当角C为钝角时证明：过A作ADCB交BC的延长线于D在Rt中ACDCACCACCDCACCACADcos)180cos(sin)180sin(在中CACCBCBACCACCACCBCBCACCDCBCACBDADABcos2coscos2sin)()sin(222222222222Cabbaccos2222bAacCBD复习引入向量法几何法坐标法例题定理小结RtABD余弦定理bAacCB证明：以CB所在的直线为X轴，过C点垂直于CB的直线为Y轴，建立如图所示的坐标系，则A、B、C三点的坐标分别为：)0,0(),0,(),sin,cos(CaBCbCbACabbaCbaCabCbCbaCbABcos2sincos2cos)0sin()cos(2222222222Cabbaccos2222复习引入向量法几何法坐标法例题定理小结利用余弦定理，可以解决：（1）已知三边，求三个角；（2）已知两边及夹角，求第三边和其他两个角.ABCabcc2=a2＋b2－2abcosC.a2＋b2－c22abcosC＝复习引入向量法几何法坐标法例题定理小结例1：在ABC中，已知a＝7，b＝10，c＝6，求A、B和C.解：b2＋c2－a22bc cosA＝＝0.725，∴A≈44°a2＋b2－c22ab cosC＝＝0.8071，∴C≈36°,∴B＝180°－(A＋C)≈100°. sinC＝≈0.5954,∴C≈36°或144°(舍).csinAa()复习引入向量法几何法坐标法例题定理小结例2：在ABC中，已知a＝2.730，b＝3.696，C＝82°28′，解这个三角形.解：由c2=a2＋b2－2abcosC,得c≈4.297.b2＋c2－a22bc cosA＝≈0.7767，∴A≈39°2′,∴B＝180°－(A＋C)＝58°30′.asinCc sinA＝≈0.6299，∴A=39°或141°(舍).()复习引入向量法几何法坐标法例题定理小结ABCOxy例3：ABC三个顶点坐标为(6，5)、(－2，8)、(4，1)，求A.解法一： AB＝√[6-(-2)]2+(5-8)2=√73,BC＝√(-2-4)2+(8-1)2=√85,AC＝√(6-4)2+(5-1)2=2√5,cosA＝＝,2ABACAB2＋AC2－BC22√365∴∴A≈84°.复习引入向量法几何法坐标法例题定理小结例3：ABC三个顶点坐标为(6，5)、(–2，8)、(4，1)，求A.ABCOy解法二：∴A≈84°.∴cosA＝＝＝.AB·ACABAC(–8)×(–2)＋3×(–4)√73·2√52√365 AB＝(–8，3)，AC＝(–2，–4).复习引入向量法几何法坐标法例题定理小结ABCOxy例3：ABC三个顶点坐标为(6，5)、(–2，8)、(4，1)，求A.αβ分析三：A=α+β,tanα=?tanβ=?tan(α+β)=复习引入向量法几何法坐标法例题定理小结解：在AOB中， |a–b|2＝|a|2＋|b|2–2|a||b|cos120°＝61,∴|a–b|＝√61.例4：已知向量a、b夹角为120°，且|a|＝5，|b|＝4，求|a–b|、|a＋b|及a＋b与a的夹角.a－ba＋bBbACa120°O复习引入向量法几何法坐标法例题定理小结∴a＋b＝√21.∴∠COA即a＋b与a的夹角约为49°. cos∠COA＝≈0.6546,a2＋a＋b2–b22aa＋b例4：已知向量a、b夹角为120...