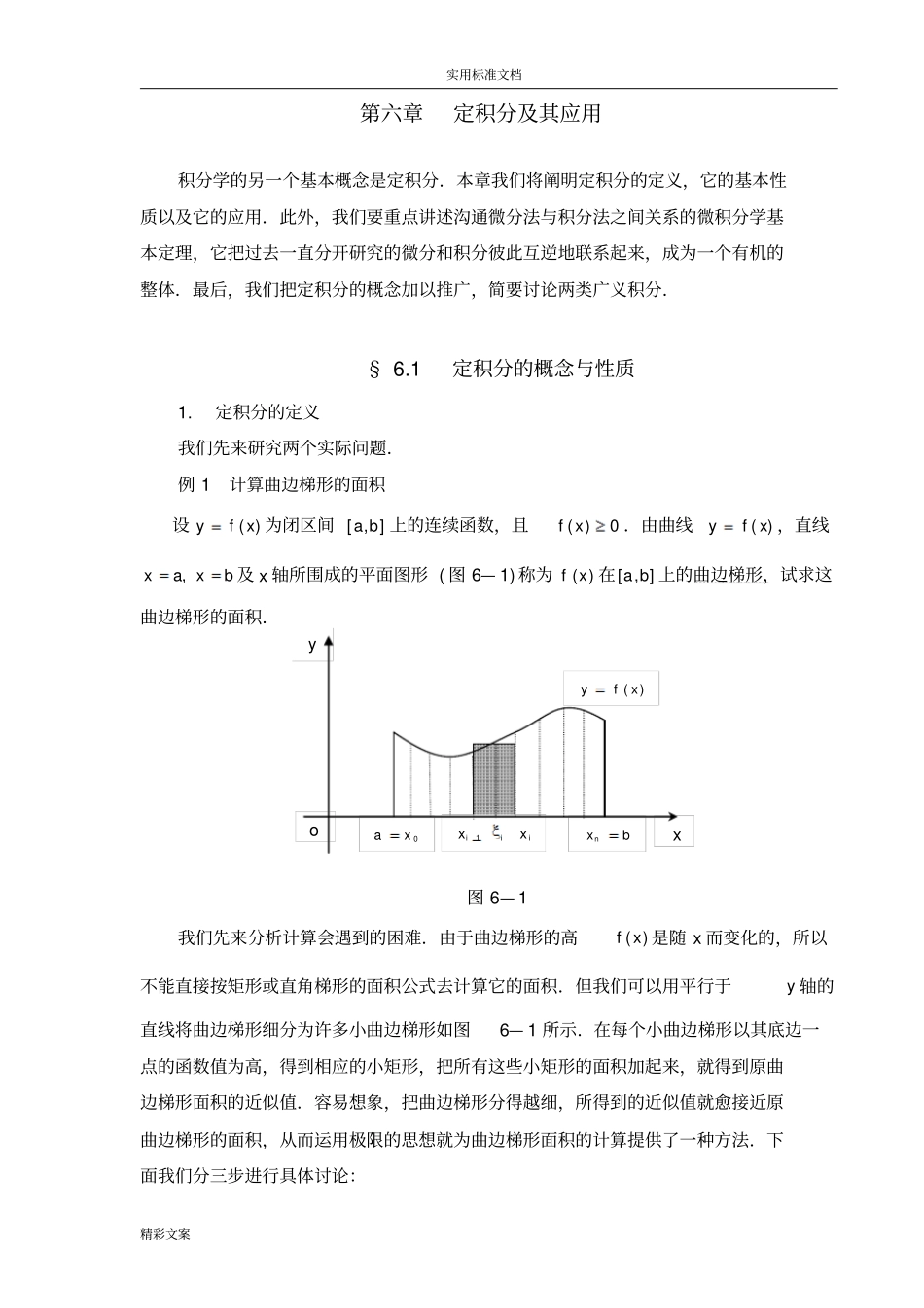
实用标准文档精彩文案xyo)(xfy0xabxniiixx1第六章定积分及其应用积分学的另一个基本概念是定积分.本章我们将阐明定积分的定义,它的基本性质以及它的应用.此外,我们要重点讲述沟通微分法与积分法之间关系的微积分学基本定理,它把过去一直分开研究的微分和积分彼此互逆地联系起来,成为一个有机的整体.最后,我们把定积分的概念加以推广,简要讨论两类广义积分.§6.1定积分的概念与性质1.定积分的定义我们先来研究两个实际问题.例1计算曲边梯形的面积设)(xfy为闭区间],[ba上的连续函数,且0)(xf.由曲线)(xfy,直线bxax,及x轴所围成的平面图形(图6—1)称为)(xf在],[ba上的曲边梯形,试求这曲边梯形的面积.图6—1我们先来分析计算会遇到的困难.由于曲边梯形的高)(xf是随x而变化的,所以不能直接按矩形或直角梯形的面积公式去计算它的面积.但我们可以用平行于y轴的直线将曲边梯形细分为许多小曲边梯形如图6—1所示.在每个小曲边梯形以其底边一点的函数值为高,得到相应的小矩形,把所有这些小矩形的面积加起来,就得到原曲边梯形面积的近似值.容易想象,把曲边梯形分得越细,所得到的近似值就愈接近原曲边梯形的面积,从而运用极限的思想就为曲边梯形面积的计算提供了一种方法.下面我们分三步进行具体讨论:实用标准文档精彩文案1nt2t1tt0taobtn(1)分割在],[ba中任意插入1n个分点bxxxxxann1210把],[ba分成n个子区间],[10xx,],[21xx,⋯,],[1nnxx,每个子区间的长度为1iiixxx),,2,1(ni.(2)近似求和在每个子区间],[1iixx),,2,1(ni上任取一点i,作和式iniixf1)((1.1)(3)取极限当上述分割越来越细(即分点越来越多,同时各个子区间的长度越来越小)时,和式(1.1)的值就越来越接近曲边梯形的面积(记作A).因此当最长的子区间的长度趋于零时,就有Axfinii1)(.例2求变速直线运动的路程设某物体作直线运动,其速度v是时间t的连续函数)(tvv.试求该物体从时刻at到时刻bt一段时间内所经过的路程s.因为)(tvv是变量,我们不能直接用时间乘速度来计算路程.但我们仍可以用类似于计算曲边梯形面积的方法与步骤来解决所述问题.(1)用分点btttttann1210把时间区间],[ba任意分成n个子区间(图6—2):],[10tt,],[21tt,⋯,],[1nntt.每个子区间的长度为1iiittt(ni,2,1).图6—2(2)在每个子区间],[1iitt(ni,2,1)上任取一点i,作和式实用标准文档精彩文案iniitv1)(.(3)当分点的个数无限地增加,最长的子区间的长度趋于零时就有stvinii1)(.以上两个问题分别来自于几何与物理中,两者的性质截然不同,但是确定它们的量所使用的数学方法是一样的,即归结为对某个量进行“分割、近似求和、取极限”,或者说都转化为具有特定结构的和式(1.1)的极限问题,在自然科学和工程技术中有很多问题,如变力沿直线作功,物质曲线的质量、平均值、弧长等,都需要用类似的方法去解决,从而促使人们对这种和式的极限问题加以抽象的研究,由此产生了定积分的概念.定义6.1.1设函数)(xf在],[ba上有定义,在),(ba内任取1n个分点bxxxxxann1210把],[ba分成n个子区间],[10xx,],[21xx,⋯,],[1nnxx,每个子区间的长度为1iiixxx),,2,1(ni.在每个子区间],[1iixx),,2,1(ni上任取一点i(称为介点),作和式iniixf1)(,并记inix1max.如果不论对],[ba怎样划分成子区间,也不论在子区间],[1iixx上怎样取介点i,只要当0时,和式(1.1)总趋于确定的值I,则称这极限值I为函数)(xf在区间],[ba上的定积分,记作badxxf)(,即iniibaxfIdxxf10)(lim)((1.2)其中)(xf称为被积函数,x称为积分变量,],[ba称为积分区间,ba,分别称为积分的下限和上限.关于定积分的定义,再强调说明几点:(1)区间],[ba划分的细密程度不能仅由分点个数的多少或n的大小来确定.因为尽管n很大,但每一个子区间的长度却不一定都很小.所以在求和式的极限时,必须要求最长的子区间的长度0,这时必然有n.(2)定义中的两个“任取”意味着这是一种具有特定结构的极限,它不同于第二实用标准文档精彩文案oyx)(xfy章讲述的函数极限.尽管和式(1.1)随着区间的不同划分及介点的不同选取而不断变化着,但当0时却都以唯一确定的值为极限.只有这时,我们才说定积分...