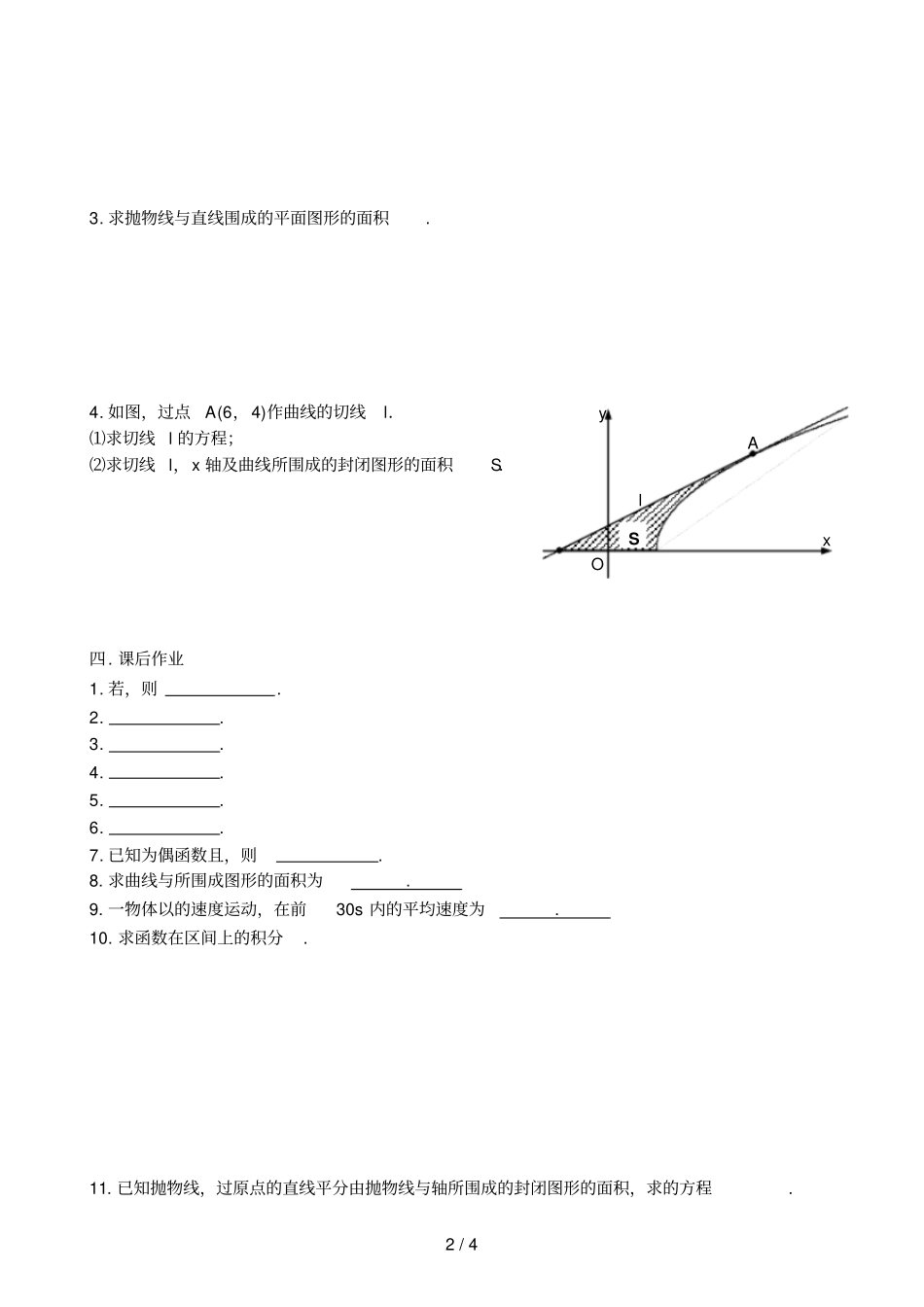
1/4第19课时定积分及其应用一.知识梳理1.定积分的概念:设函数在区间上有定义,将区间等分成分小区间,每个小区间长度为(),在每个小区间上取一点,依次为,作和.如果无限趋近于0(亦即趋向于)时,无限趋近于常数,那么称该常数为函数在区间上的定积分,记为,其中称为被积函数,称为积分区间,称为积分下限,称为积分上限,2.微积分基本定理:对于被积函数,如果,则=.3.定积分的运算性质:⑴=;⑵;⑶.4.定积分的几何意义:在区间上曲线与轴所围成图形面积的(即轴上方的面积减去轴下方的面积);⑴当在区间上大于0时,表示由直线和曲线所围成的曲边梯形的面积,这也是定积分的几何意义.⑵当在区间上小于0时,表示由直线和曲线所围成的曲边梯形的面积的.⑶当在区间上有正有负时,表示介于直线之间轴之上、之下相应的曲边梯形的面积的.5.定积分在物理中的应用:⑴匀变速运动的路程公式,作变速直线运动的物体所经过的路程,等于其速度函数在时间区间上的定积分,即.⑵变力做功公式,一物体在变力(单位:)的作用下作直线运动,如果物体沿着与相同的方向从移动到(单位:),则力所作的功为.二.基础训练1..2.已知质点的速度,则从到质点所经过的路程是.3.已知的力作用于静止的弹簧,弹簧伸长1cm,则将静止的弹簧拉长6cm,弹力所做的功为焦.4..5.已知在区间上且由直线及曲线所围成的图形面积为,则.6.由直线及曲线所围成的图形面积为,则用定积分表示,则为.三.典型例题1.求定积分⑴;⑵;⑶;⑷.2.求曲线及直线所围封闭区域的面积.2/43.求抛物线与直线围成的平面图形的面积.4.如图,过点A(6,4)作曲线的切线l.⑴求切线l的方程;⑵求切线l,x轴及曲线所围成的封闭图形的面积S.四.课后作业1.若,则.2..3..4..5..6..7.已知为偶函数且,则.8.求曲线与所围成图形的面积为.9.一物体以的速度运动,在前30s内的平均速度为.10.求函数在区间上的积分.11.已知抛物线,过原点的直线平分由抛物线与轴所围成的封闭图形的面积,求的方程.AlxySO3/412.已知方程为常数。⑴若,,求方程的解的个数的期望;⑵若内等可能取值,求此方程有实根的概率.【阅读材料】如图,用图“以直代曲”的方法计算直线x=0,x=1,y=0和曲线y=ax2(a>0)围成的阴影图形的面积.解(1)分割——把区间[0,1]等分成n个小区间:[0,1n],[1n,2n],⋯,[i-1n,in],⋯,[n-1n,nn].(2)以直代曲——△Si≈f(in)△x=ain21n.(3)作和——因为每个小矩形的面积是相应的小曲边梯形面积的近似值,所以以n个小矩形面积之和就是曲边三角形面积S的近似值,即S=△S1+△S2+⋯+△Sn=∑ni=1△Si≈an316n(n+1)(2n+1)=a6(1+1n)(2+1n).(4)逼近——当分割无限变细,即△x无限趋近于0(亦即n趋向于+∞)时,a6(1+1n)(2xyOy=ax2(a>0)x=114/4+1n)无限趋近于S,而当n趋向于+∞时,a6(1+1n)(2+1n)无限趋近于a3.由此可知S=a3.