_解直角三角形课件VIP免费

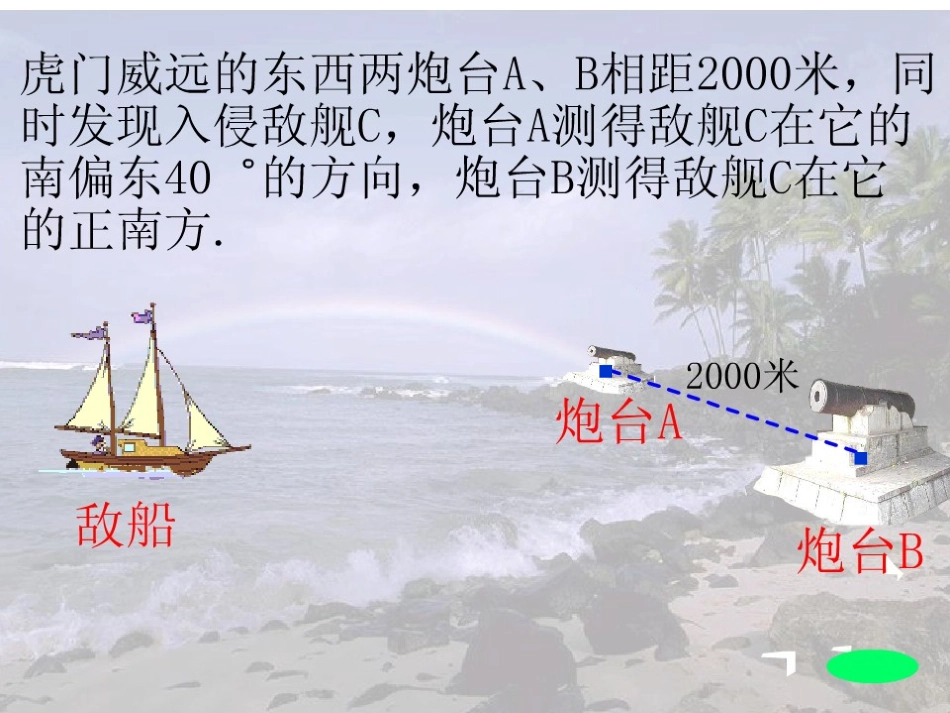
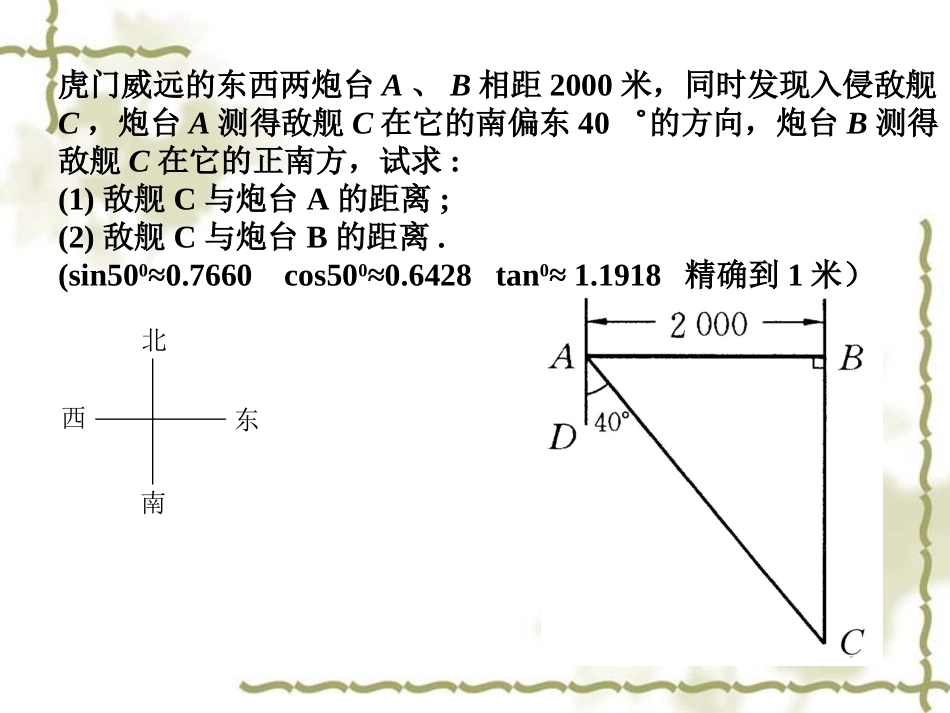
虎门威远炮台1839年，林则徐虎门销烟之后又在沿海地带整顿海防加紧训练，致使英军不敢侵犯，放弃广州而北上。鹤壁七中王静··东南西北虎门威远的东西两炮台A、B相距2000米，同时发现入侵敌舰C，炮台A测得敌舰C在它的南偏东40゜的方向，炮台B测得敌舰C在它的正南方，试求:(1)敌舰C与炮台A的距离;(2)敌舰C与炮台B的距离.(sin500≈0.7660cos500≈0.6428tan0≈1.1918精确到1米）ABabcC在直角三角形中，我们把两个锐角、三条边称为直角三角形的五个元素.图中即为直角三角形的五个元素.角∠A，∠B边a，b，c1.两锐角之间的关系:2.三边之间的关系:3.边角之间的关系∠A+∠B=900a2+b2=c2（勾股定理）ABabcC在RtABC△中，∠C=900的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=余切函数：cotA=余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=的邻边的对边正切函数：斜边的邻边余弦函数：斜边的对边正弦函数：AAAAAAAtancossin余切函数：cotA=ABabcC在直角三角形中，由已知元素求未知元素的过程，叫做解直角三角形．注意：一个直角三角形中，若已知除直角以外五个元素中的两个元素（其中必须有一个元素是边），则这样的直角三角形可解.例1、如图，在Rt△ABC中，∠C＝90°，解这个直角三角形.，6,2BCACABC26解： 在RtABC△中，AC2+BC2=AB2∴AB=22ABCC22)6()2(22 sinB=BACA22221∴∠A=60°∴∠B=30°∴AB=,A=60°,B=30°∠∠222230°例1、如图，在Rt△ABC中，∠C＝90°，解这个直角三角形.，6,2BCACABC26解：在RtABC△中∴∠A=60°∴∠B=30°∴AB=,A=60°,B=30°∠∠222230° tanB=6233BCACABAC sinB=sinBAC∴AB=222÷21第一步：利用勾股定理求第三边已知两边求解直角三角形已知一边一锐角求解直角三角形第一步：利用两锐角互余求出另一角第二步：利用已知两边的比值所对应的三角函数值，求相应的锐角第三步：由直角三角形的两锐角互余求另一锐角第二步：利用锐角三角函数及其变形求出其余两边2AC,32AB练习：1、在RtABC△中∠C=900，∠B=400AB=5则AC≈。（其中sin400≈0.745，结果保留3位有效数字）2、在RtABCA=90△∠0，，则∠B=。2,32ABAC练习：1、在RtABC△中∠C=900，∠B=400AB=5则AC≈。（其中sin400≈0.745，结果保留3位有效数字）2、在RtABCA=90△∠0，则∠B=。3.73300ABC40°5AC=AB·sin400≈50.745≈3.73※sinB=ABACABC322cotB==ACAB23233、在RtABC△中∠C=900，已知，解这个直角三角形。220c20a∴b=22)2...