同底数幂的乘法2VIP免费

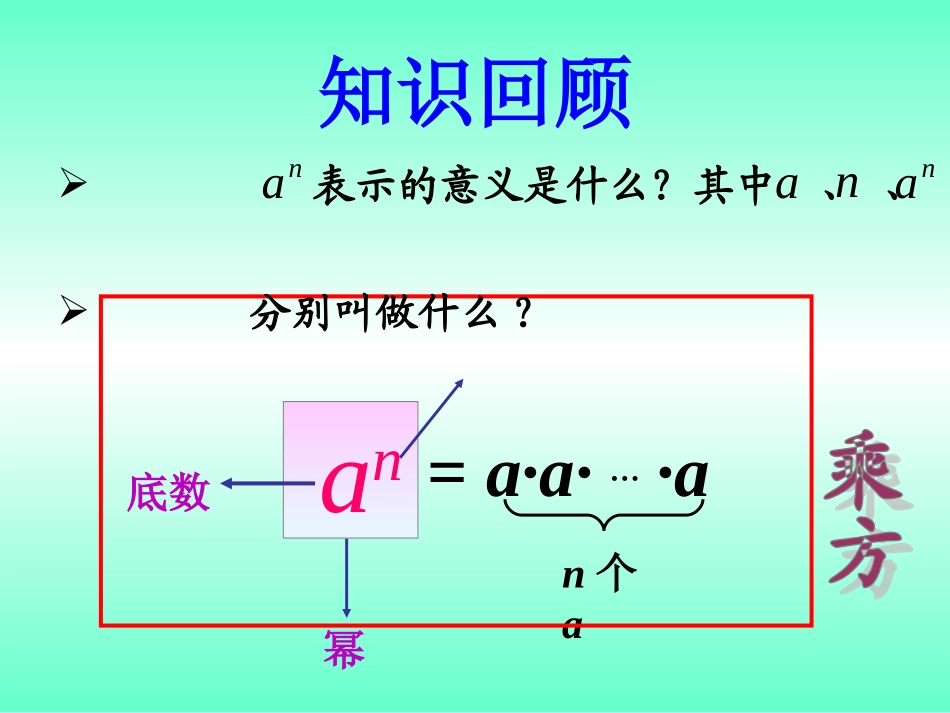
水冶镇一中牛艳丽14.1.1同底数幂的乘法学习目标1．理解同底数幂的乘法法则．2．运用同底数幂的乘法法则计算．(重点)知识回顾=a·a·…·an个aan底数幂表示的意义是什么？其中、、分别叫做什么?naanna自我预习预习课本P141～142，完成第3题．1..根据幂的意义解答(25)103×102＝10×10×10×10×10＝10()；23×22＝_＝2()；a3×a2＝(a·a·a)·()＝a()．5m·5n＝________(m，n都是正整数)．am·an＝________(m，n都是正整数)思考：观察上面各题左右两边，底数、指数有什么关系？你能得到什么结论？5555m+nam+n2×2×2×2×2a·a同底数幂的乘法公式：•am·an=am+n(m、n都是正整数)同底数幂相乘，底数不变，指数相加类比：am·an·ap＝______(m，n，p都是正整数)．__am+n+p小试牛刀选择（40）1．在等式a2·a4·()＝a11中，括号里面的式子应当是()A．a7B．a6C．a5D．a82．1000×100×10的结果是()A．106B．10×104C．100×102D．1053．计算a5·a3等于()A．a5B．a6C．a8D．a94．下列各等式中，正确的是()A．a5·a2＝a10B．a2＋a5＝a7C．a2·a5＝a7D．a2·a2＝2a2CACC你认为在运用同底数幂的乘法法则时，应注意什么问题？1.必须具备同底、相乘两个条件；2.注意am·an与am+an的区别；3.不能疏忽指数为1的情况。快速抢答(60)(1)107×103＝________；(2)a3·a5＝________；(3)x4·x5＝________；(4)x·x2·x3＝________；(5)bm·bm－1＝________；(6)(a＋2)2·(a＋2)3＝________.1010a8x9x6b2m-1(a＋2)10合作探究一(30)1.(－a)2＝____，(－a)3＝____，(x－y)2____(y－x)2，(x－y)3＝____(y－x)3.2.(－a)5·(－a)3·(－a)＝________3.－x2·(－x)3＝________a2－a9－a3＝-x5计算：(30)(1)(－5)6×59；(2)－a2·a6；(3)(a－3b)2(3b－a)3.解：(1)(－5)6×59＝56·59＝515.(2)－a2·a6＝－a8.(3)(a－3b)2(3b－a)3＝(3b－a)2(3b－a)3＝(3b－a)5.小小提升合作探究二逆用同底数幂的乘法已知ax＝2，ay＝3(x，y为正整数)，求ax＋y的值．(10)分析：ax＋y＝ax·ay.解：∵ax＝2，ay＝3，∴ax＋y＝ax·ay＝2×3＝6.规律总结：am·an＝am＋nm，n都是正整数与am＋n＝am·anm，n都是正整数都属于同底数幂乘法公式，要灵活运用学为我用(25)1．y2m＋2可写成()A．2ym＋1B．y2m·y2C．y2·ym＋1D．y2m＋y22．(1)x5·()＝x8；(2)x·x3·()＝x7.3．已知2x＝5，求2x＋3的值．Bx3x3解：2x+3＝2x·23＝5×8＝401．下列计算中错误的是()A．am·a3＝a3mB．x5＋x5＝2x5C．x5·x5＝x10D．am－2·am＋2＝a2m2．若ym－2·ym＋2＝y6，则m＝()A．8B．4C．6D．33．(1)－x7·x(－x)3＝________；(2)xm·()＝x3m.4．若am＝7，an＝6，则am＋n＝________.当堂测试(25)ADx11x2m42直击中考(15)1.已知am＝2，am＋n＝10，求an的值．解：∵am·an＝am＋n＝10，am＝2∴2·an＝10∴an＝5(20)2.计算：(1)x·xm－xm＋1；(2)y·yn＋1－yn·y2.本课小结本节课你有什么收获？1.am·an=am+n(m、n都是正整数)2.am·an·ap＝__am+n+p______(m，n，p都是正整数)．既可以正用也可以逆用1.必做题：练习册75页1-8题2.选做题：练习册75页学习拓展布置作业•不经历风雨，怎能见彩虹!•加油，相信你一定会成功!