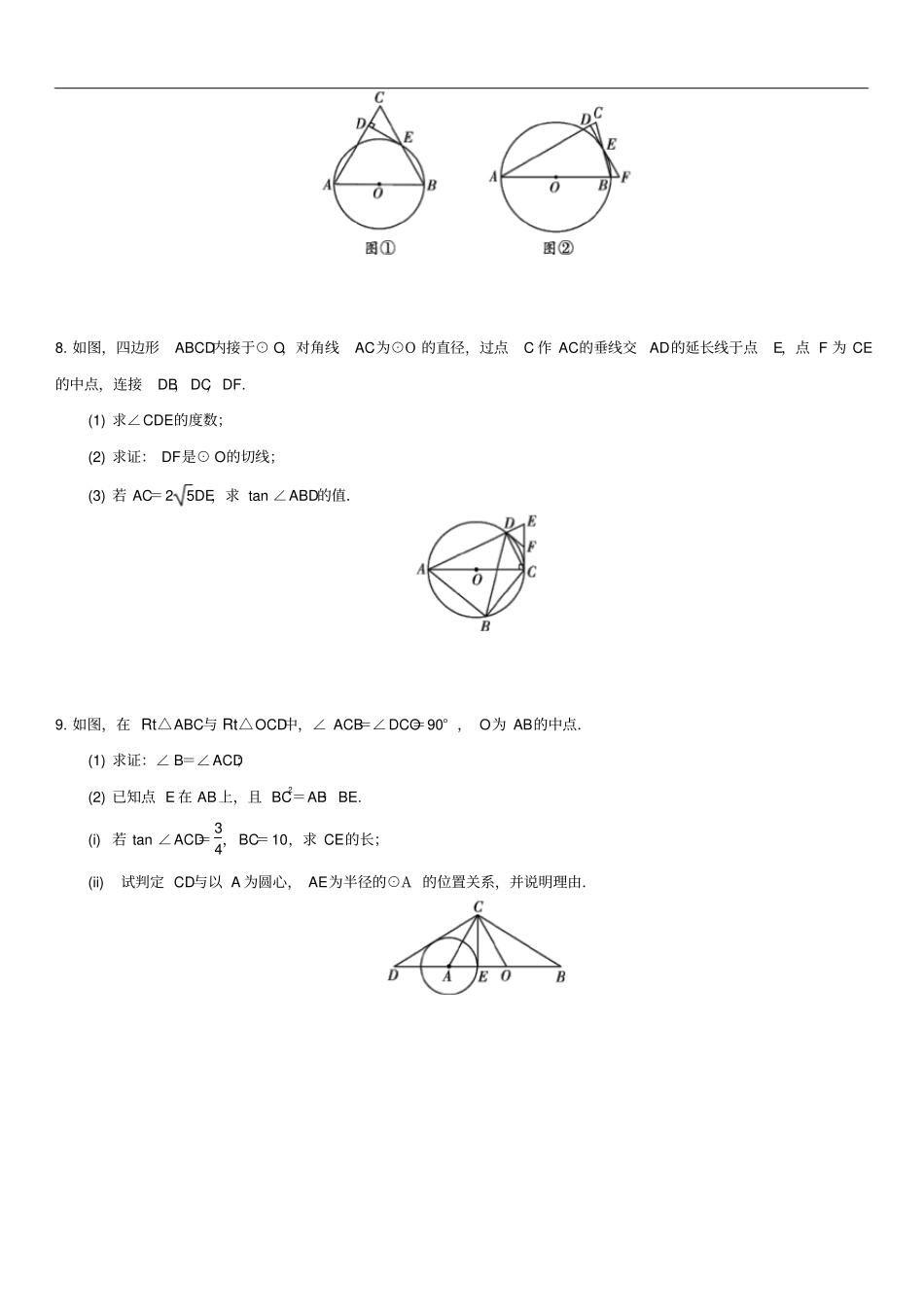
圆的证明与计算专题1.如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.(1)求证:△ABC是等边三角形;(2)若∠PAC=90°,AB=23,求PD的长.2.如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.(1)求证:直线CD是⊙O的切线;(2)如果D点是BC的中点,⊙O的半径为3cm,求DE︵的长度.(结果保留π)3.如图,点D是等边三角形ABC的外接圆上一点,M是BD上一点,且满足DM=DC,点E是AC与BD的交点.(1)求证:CM∥AD;(2)如果AD=1,CM=2.求线段BD的长及△BCE的面积.4.如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线交于点E,且∠A=∠EBC.(1)求证:BE是⊙O的切线;(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG·BA=48,FG=2,DF=2BF;求AH的值.5.如图,AB为△ABC外接圆⊙O的直径,点P是线段CA延长线上一点,点E在圆上且满足PE2=PA·PC,连接CE,AE,OE,OE交CA于点D.(1)求证:△PAE∽△PEC;(2)求证:PE为⊙O的切线;(3)若∠B=30°,AP=12AC,求证:DO=DP.6.如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的⊙O与AD,AC分别交于点E,F,且∠ACB=∠DCE.(1)判断直线CE与⊙O的位置关系,并证明你的结论;(2)若tan∠ACB=22,BC=2,求⊙O的半径.7.如图①,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.(1)试判断△ABC的形状,并说明理由;(2)如图②,若线段AB、DE的延长线交于点F,∠C=75°,CD=2-3,求⊙O的半径和BF的长.8.如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.(1)求∠CDE的度数;(2)求证:DF是⊙O的切线;(3)若AC=25DE,求tan∠ABD的值.9.如图,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.(1)求证:∠B=∠ACD;(2)已知点E在AB上,且BC2=AB·BE.(i)若tan∠ACD=34,BC=10,求CE的长;(ii)试判定CD与以A为圆心,AE为半径的⊙A的位置关系,并说明理由.参考答案1.(1)证明:由题意可得:∠BPC=∠BAC,∠APC=∠ABC, ∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC是等边三角形.(2)解: ∠PAC=90°,∴PC是圆的直径,∴∠PBC=90°,∴∠PBD=90°, △ABC是等边三角形,∴AB=BC=23, ∠CPB=60°,∴PB=23tan60°=2, ∠APC=60°,∴∠DPB=180°-60°-60°=60°,∴PD=2PB=4.2.(1)证明: CA切⊙O于点A,∴∠CAO=90°. OC平分∠AOD,∴∠AOC=∠DOC,在△AOC和△DOC中,,∴△AOC≌△DOC(SAS),∴∠CDO=∠CAO=90°, OD是⊙O的半径,∴CD是⊙O的切线.(2)解:由(1)知:OD⊥BC,又 D是BC的中点,∴OD是BC的垂直平分线,∴OC=OB,∴∠BOD=∠DOC=∠COA=13×180°=60°,∴∠DOE=60°,∴DE︵的长度为60180π×3=π.3.(1)证明: △ABC是等边三角形,∴∠BAC=∠ACB=60°,∴∠BDC=∠BAC=60°,∠ADB=∠ACB=60°,∴∠ADC=120°, DM=DC,∴△DMC是等边三角形,∴∠MCD=60°,∴∠MCD+∠ADC=180°,∴CM∥AD.(2)解: BC=AC,∠ADC=∠BMC=120°,∠CBM=∠CAD,∴△ADC≌△BMC,∴AD=MB=1,∴BD=BM+MD=AD+CM=1+2=3, CM∥AD,∴∠CAD=∠ACM,∠ADE=∠EMC,∴△ADE∽△CME,∴ADCM=AEEC=DEEM=12,∴S△ADE=14S△EMC, S△CMD=12×3×2=3,∴S△EMC=23S△CMD=233,S△EDC=13S△CDM=33,∴S△ADE=14S△EMC=36,∴S△ADC=S△ADE+S△DCE=36+33=32,∴S△BCE=S△BMC+S△MCE=S△ADC+S△CME=32+233=763.4.解:(1)连接DC, DB是⊙O的直径,∴∠DCB=90°,∴∠D+∠DBC=90°, ∠D=∠A,∠EBC=∠A.∴∠D=∠EBC,∴∠EBC+∠DBC=90°,即∠DBE=90°,∴BE是⊙O的切线.(2) CG∥EB,∴∠BCG=∠EBC,∴∠A=∠BCG,又 ∠CBG=∠ABC,∴△ABC∽△CBG,∴BCBG=ABBC,即BC2=BG·AB=48,∴BC=43, CG∥EB,∴CF⊥BD,∴∠CFB=∠DCB=90°,又 ∠CBF=∠DBC,∴Rt△BFC∽Rt△BCD,∴BFBC=BCBD,∴BC2=BF·BD...