高二数学选修2-2~322复数的四则运算VIP免费

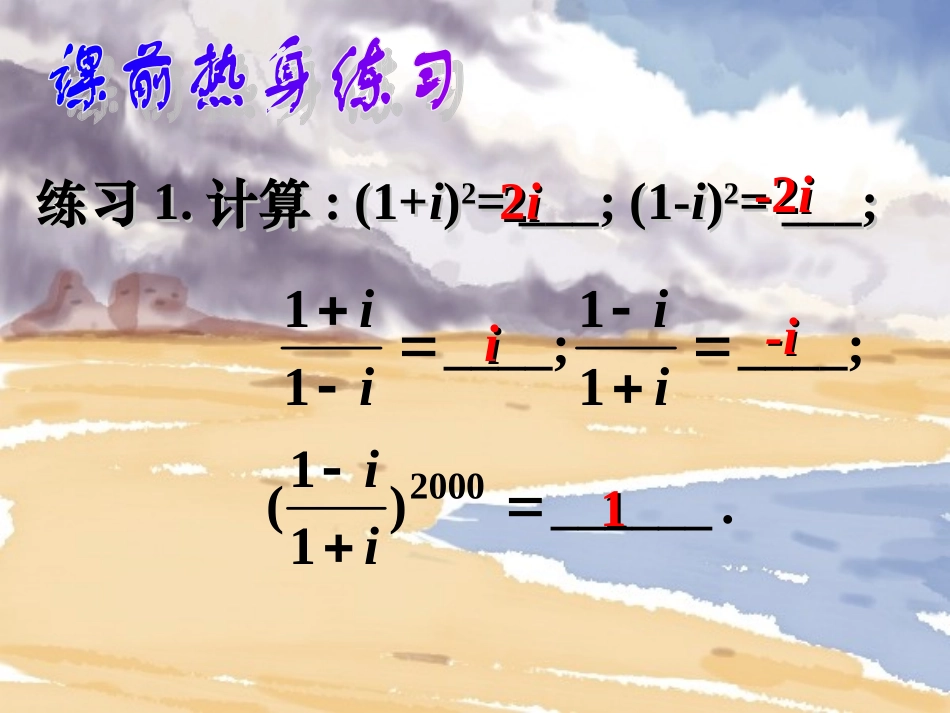
25年1月8日25年1月8日苏教高中数学选修苏教高中数学选修2-22-2教学目标：教学目标：（（11）理解复数代数形式的四则运算法则；）理解复数代数形式的四则运算法则；（（22）能运用运算律进行复数的四则运算；）能运用运算律进行复数的四则运算；练习练习1.1.计算计算:(1+:(1+ii))22=___;(1-=___;(1-ii))22=___;=___;____;11____;11iiii.______)11(2000ii22ii-2-2iiii-i-i118)23123(.2ii计算练习883i-i的值时，求当练习1213.50100zziz11、复数的加法与减、复数的加法与减法法idbcadicbia即即::两个复数相加两个复数相加((减减))就是实部与实部就是实部与实部,,虚虚部与虚部分别相加部与虚部分别相加((减减).).22、复数的乘法法则、复数的乘法法则ibcadbdacdicbia)()(即即::类似于多项式的乘类似于多项式的乘法法..______720063210的值等于求例iiiii)(0321Nniiiiinnnn可以证明的性质，解：根据02004321iiii2006200520043210iiiiiii则有2006200520043210)(iiiiiii2100iii101ii).4,,,(0:0,4a个连续的整数为任意其中即为个连续的整数的幂的和的任意一般结论：对dcbaiiiiidcb33、复数的乘方、复数的乘方对任何及，有对任何及，有Czzz21,,Nnm,nmnmzzzmnnmzz)(nnnzzzz2121)(iiiiiinnnn3424144,1,,1一般地，如果，一般地，如果，有有ii幂的周期性：幂的周期性：Nn((复数的乘方是相同复数的复数的乘方是相同复数的积积))0321nnnniiiii可有的周期性，幂根据)Z(n2222acbdbcadabicdiicdcd设设,,是任意两个复是任意两个复数，则它们的商为：数，则它们的商为：biaz1dicz2即即先把除式写成分式的形式先把除式写成分式的形式,,再把分子与分母再把分子与分母都乘以分母的共轭复数都乘以分母的共轭复数,,化简后写成代数形式化简后写成代数形式((分母实数化分母实数化).).44、复数的除法法则、复数的除法法则思考思考::除式改成分式后如何除式改成分式后如何把分母实数化？把分母实数化？①①如果如果nnN*∈N*∈有有::ii44nn=1;=1;ii44nn+1+1==ii,,ii44nn+2+2=-1;=-1;ii44nn+3+3=-=-ii..((事实上可以把它推广到事实上可以把它推广到nnZ.∈Z.∈））②设,则有:i2321.01;;12__23__事实上事实上,,与统称为与统称为11的立方虚根的立方虚根,,而且对于而且对于,,也有类似于上面的三个等式也有类似于上面的三个等式..__③.11;11;1;2)1(2iiiiiiiiii55、一些常用的计算结果、一些常用的计算结果::223.:()()(,).abiabiababR例证明思考思考::写出上式的逆向表达式并指出其意义写出上式的逆向表达式并指出其意义??),())(()1(22Rbabiabiaba其中(2)(2)此为在复数范围内因式分解的依据此为在复数范围内因式分解的依据..44:1ba在复数范围内因式分解示例abcbaxxxEx2)3(52)2(4)1(122222：在复数范围内分解因式0169)2(1)1(224xxEx方程的根：在复数范围内写出下列.41)1)(1)(1)(1(44个四次方根的内并由此写出在复数范围求证：ixixixixx.44,11404,)1(4个根在复数范围内有也即和个根，即内应有在复数范围并由上式可知此式可按从右向左证明分析：ixixx.2222,2222,2222,2222:4101044,2,04)2(444iiiitttxx个四次方根为在复数范围内的这样可得到即则有令中在方程232132:,2213(1),22(2)1(3)10ii若则有：，。?,:上述的结论还会成立吗换成若把思考特殊运算：111222iii220例5:求()()...()的值.20(120)21021052105426112112212()22iiiiiii1＋2＋3＋＋20解：原式()()=()()4562200832(1)?;????ni1例题6：若=-，2求：(2)...