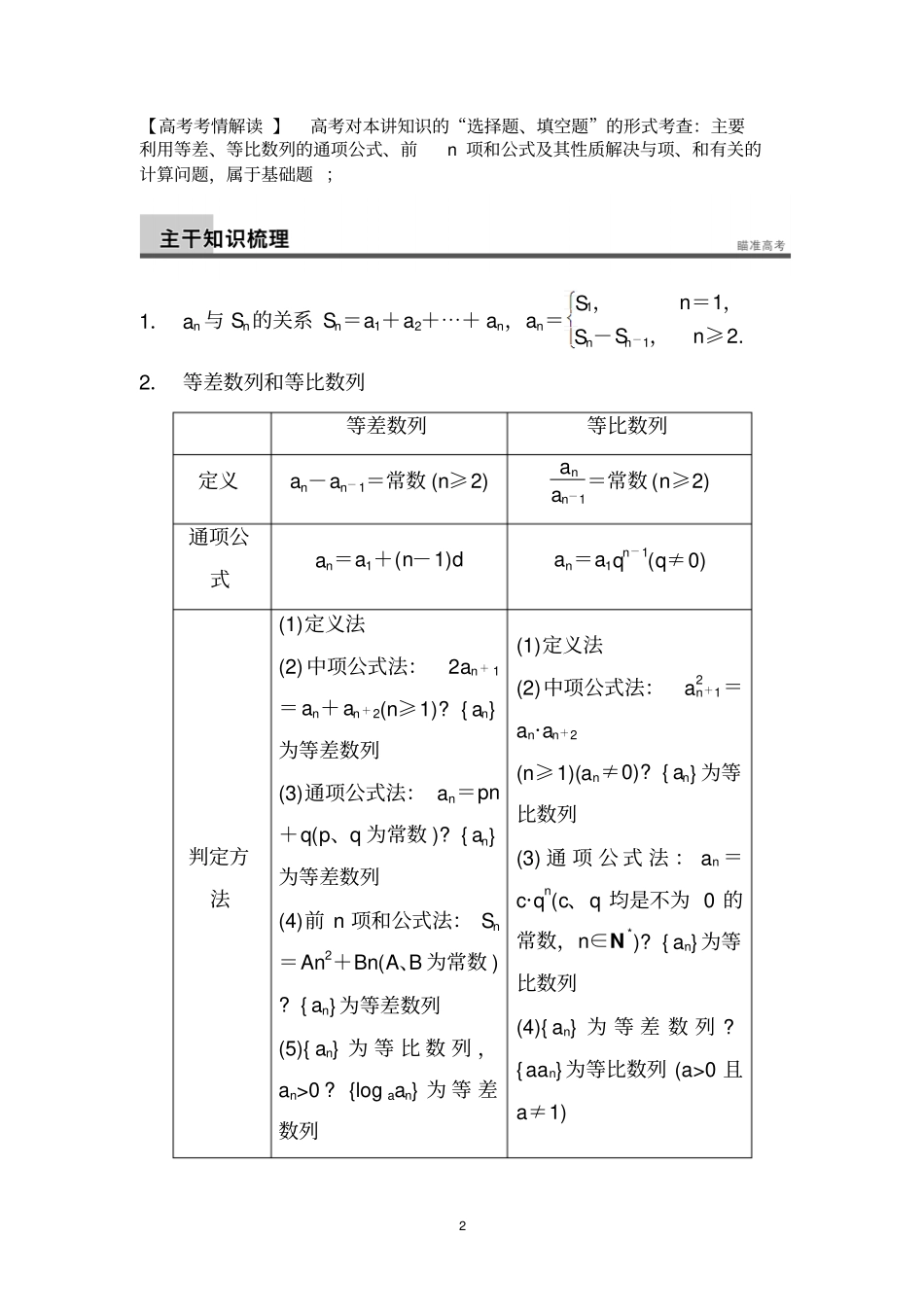
1数列专题复习【近四年广东高考】201120122013201419分19分19分19分一、“选择,填空题”回顾:(2011年高考广东卷第11小题)已知na是递增等比数列,2432,4,aaaq则此数列的公比;(2012年高考广东卷第12小题)若等比数列}{na满足2142aa,则5231aaa;(2013年高考广东卷第11小题)设数列na是首项为1,公比为2的等比数列,则1234aaaa;(2014年高考广东卷第13小题)等比数列na的各项均为正数,且154aa,则2122232425logloglogloglogaaaaa;2【高考考情解读】高考对本讲知识的“选择题、填空题”的形式考查:主要利用等差、等比数列的通项公式、前n项和公式及其性质解决与项、和有关的计算问题,属于基础题;1.an与Sn的关系Sn=a1+a2+⋯+an,an=S1,n=1,Sn-Sn-1,n≥2.2.等差数列和等比数列等差数列等比数列定义an-an-1=常数(n≥2)anan-1=常数(n≥2)通项公式an=a1+(n-1)dan=a1qn-1(q≠0)判定方法(1)定义法(2)中项公式法:2an+1=an+an+2(n≥1)?{an}为等差数列(3)通项公式法:an=pn+q(p、q为常数)?{an}为等差数列(4)前n项和公式法:Sn=An2+Bn(A、B为常数)?{an}为等差数列(5){an}为等比数列,an>0?{logaan}为等差数列(1)定义法(2)中项公式法:a2n+1=an·an+2(n≥1)(an≠0)?{an}为等比数列(3)通项公式法:an=c·qn(c、q均是不为0的常数,n∈N*)?{an}为等比数列(4){an}为等差数列?{aan}为等比数列(a>0且a≠1)3性质(1)若m、n、p、q∈N*,且m+n=p+q,则am+an=ap+aq(2)an=am+(n-m)d(3)Sm,S2m-Sm,S3m-S2m,⋯仍成等差数列(1)若m、n、p、q∈N*,且m+n=p+q,则am·an=ap·aq(2)an=amqn-m(3)等比数列依次每n项和(Sn≠0)仍成等比数列前n项和Sn=na1+an2=na1+nn-12d(1)q≠1,Sn=a11-qn1-q=a1-anq1-q(2)q=1,Sn=na1考点一.基础公式训练等差数列的通项公式:1(1)naand;()nmaanmd等比数列的通项公式:11nnaaq;nmnmaaq等差数列前n和公式:11()(1)22nnnaannSnad。等比数列前n项和公式:111(q1)(1q)(q1)11nnnnasaaqaqq1:在等差数列na中,若,,3d165aaa1021则1a的值为()A.1B.2C.3D.42若等差数列{}na的前5项和525S,且23a,则7a()A.12B.13C.14D.153.已知{an}是等比数列,a2=2,a5=14,则公比q等于().A.-12B.-2C.2D.124.设Sn为等比数列{an}的前n项和,8a2+a5=0,则S5S2=().A.-11B.-8C.5D.114考点二.等差中项,等比中项a,A,b成等差数列2abA或者2A=a+b。若G2=a·b(ab≠0),那么G叫做a与b的等比中项.5.等差数列{an}的前n项和记为Sn,若3711aaa为一个确定的常数,则下列各数中也是常数的是()A.S6B.S11C.S12D.S136.已知正项数列na的前n项和为ns,且满足)(2ns2ssn21n21-n2,已知1a1a21,,求通项na的表达式考点三.等差数列的性质:(1).在等差数列na中,相隔等距离的项组成的数列是等差数列,如:1a,3a,5a,7a,⋯⋯;3a,8a,13a,18a,⋯⋯;(2).在等差数列na中,若m,n,p,qN且mnpq,则mnpqaaaa;(3).设数列{}na是等差数列,且公差为d,(Ⅰ)若项数为偶数,设共有2n项,则①S偶-S奇nd;②1nnSaSa奇偶;(Ⅱ)若项数为奇数,设共有21n项,则①S偶S奇naa中;②1SnSn奇偶。(4)232nnnnnSSSSS,,,仍为等差数列;数列{}nab(b,为常数)仍为等差数列,公差为d.等比数列的性质:(5)若{an}为等比数列,且k+l=m+n(k,l,m,n∈N+),则ak·al=am·an.(6)公比不为-1的等比数列{an}的前n项和为Sn,则Sn,S2n-Sn,S3n-S2n仍成等比数列,其公比为qn.7.在等差数列na中,已知12aa54,那么,它的前8项和8s等于()A.12B.24C.36D.4858.有两个等差数列na,nb,其前n项和分别为nnTS,,若,3n2n7nnTS求55ba9.一个等差数列的前四项之和为21,末四项之和为67,前n项和为286,则项数n为()A.24B.26C.27D.2810.在项数为2n+1的等差数列中,所有奇数项的和为165,所有偶数项的和为150,则n等于()A.9B.10C.11D.1211.在等差数列na中,若4,184SS,则20191817aaaa的值为()A9B12C16D17考点四.数列最值(1)10a,0d时,nS有最大值;10a,0d时,nS有最小值;(2)nS最值的求法:①若已知nS,可用二次函数最值的求法...