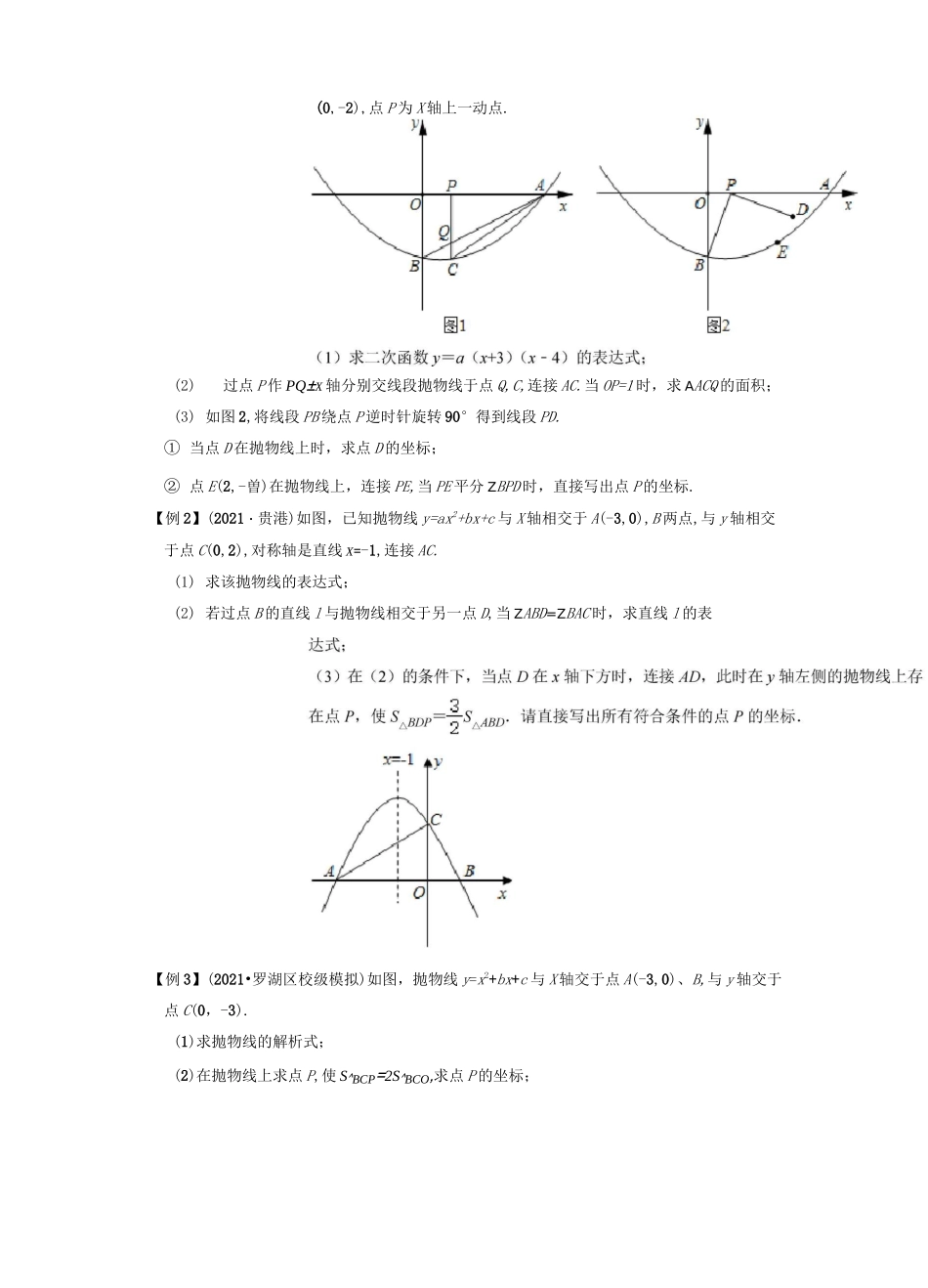
(2021-兰州中考真题)【佃(2021*^港中考真题)【例釘(20210,连接AQ,线段AQ与线段OC交于点E,OEVEC,且OE・EC=2,连接PQ,求线段PQ的长;(3)连接AC,PC,试探究:是否存在点P,使得ZPCQ与ZBAC互为余角?若存在,求出点P的坐标;若不存在,请说明理由.\/°;C7【例5】(2020•十堰)已知抛物线y=ax2-2ax+c过点A(-1,0)和C(0,3),与x轴交于另一点B,顶点为D.(1)求抛物线的解析式,并写出D点的坐标;(2)如图1,E为线段BC上方的抛物线上一点,EF丄BC,垂足为F,EM丄x轴,垂足为M,交BC于点G.当BG=CF时,求AEFG的面积;(3)如图2,AC与BD的延长线交于点H,在x轴上方的抛物线上是否存在点P,使ZOPB=ZAHB?若存在,求出点P的坐标;若不存在,请说明理由.1【例6】(2020•包头)如图,在平面直角坐标系中,抛物线y=3X12-2x经过坐标原点,与x轴正半轴交于点A,该抛物线的顶点为M,直线y=-2x+^经过点A,与y轴交于点B,连接OM.(1)求b的值及点M的坐标;(2)将直线AB向下平移,得到过点M的直线y=mx+n,且与x轴负半轴交于点C,取点D(2,0),连接DM,求证:ZADM-ZACM=45°;(3)点E是线段AB上一动点,点F是线段OA上一动点,连接EF,线段EF的延长线与线段OM交于点G.当ZBEF=2ZBAO时,是否存在点E,使得3GF=4EF?若存在,求出点E的坐标;若不存在,请说明理由.(1)若点A的坐标为(-4,-2),求点C的坐标;1(2021•海陵区一模)如图,点C(0,丄)(aV0)是y轴负半轴上的一点,经过点C作a2直线,与抛物线y=^x2交于A、B两点(点A在点B的左侧),连接OA、OB,设点A的横坐标为m(m<0).(2)若AC:BC=1:2,m=-1,求a的值,并证明:ZAOB=90°;(3)若AC:BC=1:k(k>1),问“ZAOB=90°”这一结论还成立吗?试说明理由.\O/\2.(2021•郫都区模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与轴交于A(-1,0),B(4,0),与y轴交于点C(0,-3),连接AC、BC.(1)求抛物线的函数表达式;(2)如图1,点D是抛物线上位于第四象限内的一点,连接AD,点E是AD的中点,连接BE、CE,求ABCE面积的最小值;(3)如图2,点P是抛物线上位...