应用举例距离VIP免费

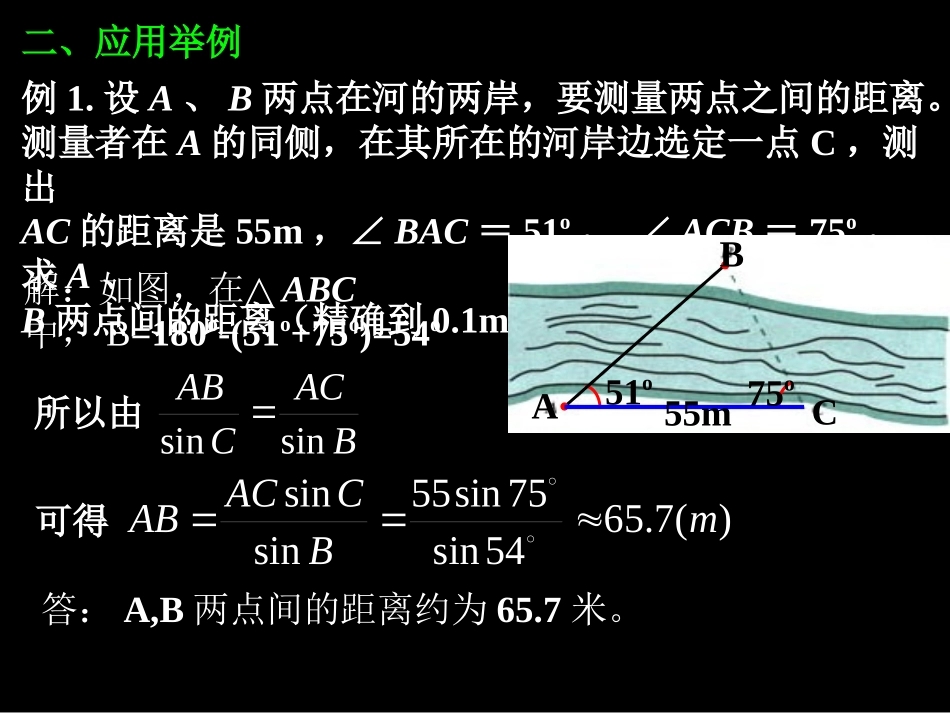
一、基本概念解斜三角形中的有关名词、术语：（1）坡度：斜面与地平面所成的角度。（2）仰角和俯角：在视线和水平线所成的角中，视线在水平线上方水平线上方的角叫仰角仰角，视线在水平水平线下方线下方的角叫俯俯角角。（3）方位角：从正北方向顺时针转到目标方向的夹角。（4）方向角：从指定方向线到目标方向线的水平角。（5）视角：由物体两端射出的两条光线在眼球内交叉而成的角练习：两灯塔A、B与海洋观察站C的距离都等于akm,灯塔A在观察站C的北偏东30°，灯塔B在观察站C南偏东60°，则A、B之间的距离为多少？2a例1.设A、B两点在河的两岸，要测量两点之间的距离。测量者在A的同侧，在其所在的河岸边选定一点C，测出AC的距离是55m，∠BAC＝51o，∠ACB＝75o，求A、B两点间的距离（精确到0.1m）二、应用举例51o75o55m解：如图，在△ABC中，B=180o-(51o+75o)=54o所以由sinsinABACCB可得sin55sin7565.7()sinsin54ACCABmB答：A,B两点间的距离约为65.7米。ABCABCD为了测定河对岸两点A、B间的距离,在岸边选定1公里长的基线CD,并测得∠ACD=90o,∠BCD=60o，∠BDC=75o，∠ADC=30o，求A、B两点的距离.三、练习二、应用举例ABCD解：如图，测量者可以在河岸边选定两点C、D，设CD=a，∠BCA=α，∠ACD=β，∠CDB=γ，∠ADB=δαβγδa例2.A、B两点都在河的对岸（不可到达），设计一种测量两点间的距离的方法。)sin()sin()(180sin)sin(aaAC)sin(sin)(180sinsinaaBCcos222BCACBCACAB如图，一艘船从C处以30nmile/h的速度往北偏东15o的A岛行驶，若船在C处测得B岛在北偏西30o的方向，行驶20min后在D处测得B岛在北偏西45o的方向，到达A岛后又测得B岛在北偏西60o的方向，试求A岛与B岛的距离。ABCD60o45o30o解：依题意可得，∠BCD=45o，∠BDA=60o，∴∠CBD=∠BDA-∠BCD=15o，13010nmile3CD10sin45sin15BD由可得20262BD又∵∠BAD=180o-60o-15o=105osin60sin105sin75ABBDBD20246262106AB化简得106nmile.答：两岛的距离为三、练习nmile/h即是：海里/每小时海里是长度单位，其单位符号为(nmile)，1nmile=1852m(只适用于航程)一海里约为3.7里。节是速度单位，单位符号为(kn)，1kn=1nmile/h=(1852/3600)m/s即:1节=1海里/1小时=0.514m/s1.分析：理解题意，画出示意图2.建模：把已知量与求解量集中在一个三角形中3.求解：运用正弦定理和余弦定理，有顺序地解这些三角形，求得数学模型的解。4.检验：检验所求的解是否符合实际意义，从而得出实际问题的解。实际问题→数学问题（三角形）→数学问题的解（解三角形）→实际问题的解解斜三角形应用题的一般步骤是：四、小结方法：练习1.一艘船以32.2nmile/h的速度向正北航行。在A处看灯塔S在船的北偏东20o的方向，30min后航行到B处，在B处看灯塔在船的北偏东65o的方向，已知距离此灯塔6.5nmile以外的海区为航行安全区域，这艘船可以继续沿正北方向航行吗？11545sin2016.1sin207.787()sin45sin45,sin657.06()6.5ASBSBASABSBnmileSABhhSBnmilehnmile解：在中，＝，，由正弦定理得设点到直线的距离为则此船可以继续沿正北方向航行答：此船可以继续沿正北方向航行练习2.自动卸货汽车的车厢采用液压机构。设计时需要计算油泵顶杆BC的长度．已知车厢的最大仰角是60°，油泵顶点B与车厢支点A之间的距离为1.95m，AB与水平线之间的夹角为6°20’，AC长为1.40m，计算BC的长（精确到0.01m）．6620最大角度最大角度最大角度最大角度CAB已知△ABC中AB＝1.95m，AC＝1.40m，夹角∠CAB＝66°20′，求BC．解：由余弦定理，得答：顶杆BC约长1.89m。五、作业P19习题1.2A组13