国培作业开课锐角三角函数复习VIP免费

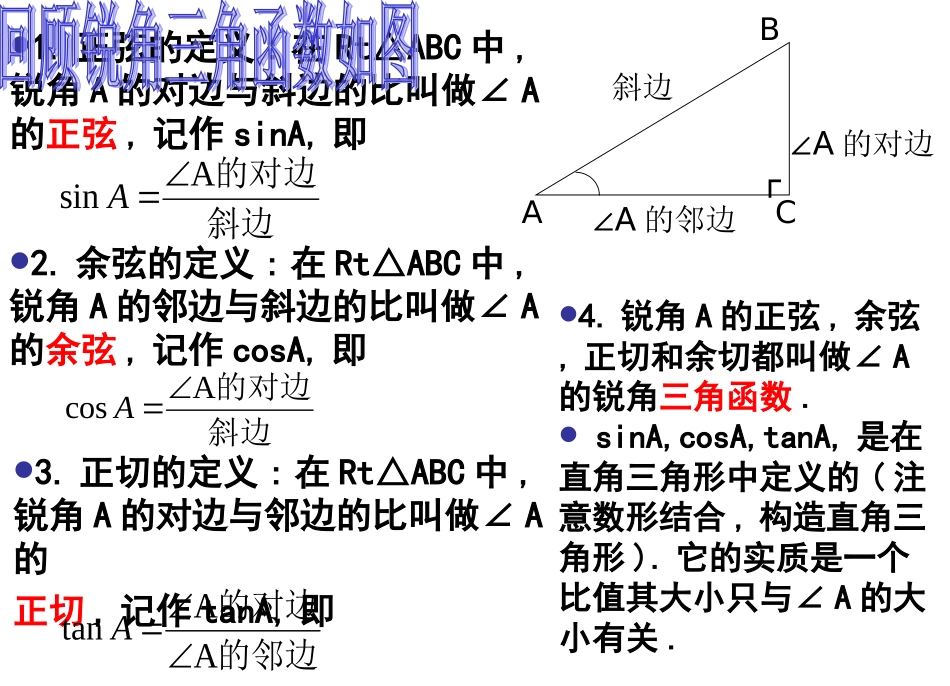
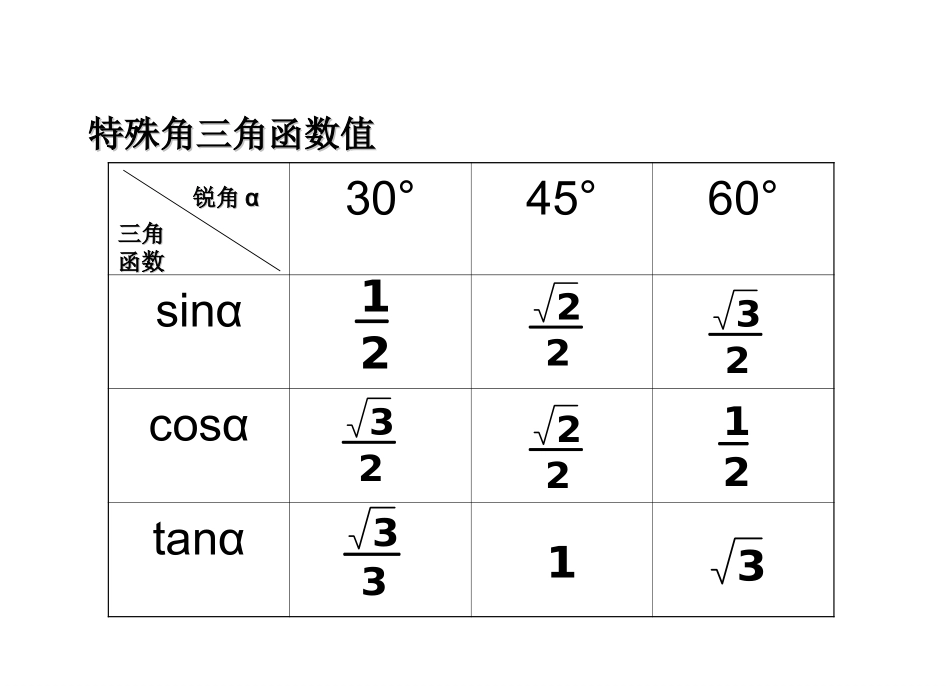
锐角三角函数（复习课）（新人教版）友联中学冯昭纯1.正弦的定义:在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即2.余弦的定义:在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即斜边的对边AsinA斜边的对边AcosA3.正切的定义:在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即的邻边的对边AAtanAABC∠A的对边∠A的邻边┌斜边4.锐角A的正弦,余弦,正切和余切都叫做∠A的锐角三角函数.sinA,cosA,tanA,是在直角三角形中定义的(注意数形结合,构造直角三角形).它的实质是一个比值其大小只与∠A的大小有关.30°45°60°sinαcosαtanα1212222232323331三角三角函数函数锐角锐角αα特殊角三角函数值特殊角三角函数值练习：31212321232121212322212解：原式121221·浙江教育版在RtABC△中，∠C为直角，∠A、∠B为锐角，它们所对的边分别为c、a、b，其中除直角c外，其余的5个元素之间有以下关系：⑴三边之间的关系：222cba⑵锐角之间的关系：90BA⑶边角之间的关系：;tan,cos,sinbacbAcaA.tan,cos,sinabcaBcbBABbac┏C⌒对边邻边斜边·浙江教育版解直角三角形的类型在RtABC△中，∠C=90°：⑴已知∠A、c,则a=__________;b=_________。⑵已知∠A、b,则a=__________;c=_________。⑶已知∠A、a，则b=__________;c=_________。⑸已知a、b，则c=__________。⑷已知a、c，则b=__________。ABbac┏C⌒对边邻边斜边已知一锐角、斜边，求对边，用锐角的正弦；求邻边，用锐角的余弦。已知一锐角、邻边，求对边，用锐角的正切；求斜边，用锐角的余弦。已知一锐角、对边，求邻边，用锐角的正切；求斜边，用锐角的正弦。AcsinAccosAbtanAbcosAatanAasin22ba22ac练习：3103545152►类型之一：利用直角三角形解决和高度有关的问题命题角度：1.计算高度（树高、楼高、山高、旗杆高等）2.根据材料提供的生活背景，画出几何图形，并把实际问题数学化，将数学问题转化为直角三角形问题。解直角三角形的实际应用仰角和俯角铅直线水平线视线视线仰角俯角在进行测量时，从下向上看，视线与水平线的夹角叫做仰角；从上往下看，视线与水平线的夹角叫做俯角.练习11、（2007年昆明）如图，AB和CD是同一地面上的两座相距36米的楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°，楼底D的俯角为30°，求楼CD的高？(结果保留根号)300450ABCD36EABDCE分析:如图,在RtACE△中,CAE∠=45°，AE＝36．所以可以利用解直角三角形的知识,求出CE,类似地可以求出DE,进而求出CD解：过A作AECD⊥于E,∠CAE=45°,DAE=30∠°，BD=AE＝36．45tan36tanCAEAECE3613630tan36tanDAEAEDE312333631236DECECDABDCE45°30°36答:楼CD高为m)31236( ►类型之二：利用直角三角形解决航海问题解题关键：弄清楚方位角和做直角三角形,将实际问题转化为常见的图形（一个或两个直角三角形）来解，会判断（如会不会触礁等）的实际问题解直角三角形的实际应用•指南或指北的方向线与目标方向线构成小于90°的角,叫做方位角.•如图：点A在O的北偏东30°•点B在点O的南偏西45°（西南方向）30°45°BOA东西北南方位角答：货轮无触礁危险。AD≈12×1.732=20.784>20解：过点A作ADBC⊥于D,ABDCNN130˚60˚24海里X在RtADC△中， tanDCA=∠——∴AD=tan60°x=xADDC3设CD=x,2、(2006贵州)如图，海岛A四周20海里周围内为暗礁区，一艘货轮由东向西航行，在B处见岛A在北偏西60˚，航行24海里到C，见岛A在北偏西30˚，货轮继续向西航行，有无触礁的危险？（参考数据：）30˚60˚732.13在RtADB△中， tan30˚=——ADBD∴BD=3x∴24=3x-x，解得x=12 BC=24，且BC=BD-CD►类型之三：利用直角三角形解决有关坡度的实际问题命题角度：1.根据材料提供的生活背景，画出几何图形，并把实际问题数学化；2.理解坡度的概念，会通过作适当的辅助线构造直角三角形，使之转化为解直角三角形的计算问题而达到解决实际问题解直角三角形的实际应用坡度（坡比）：坡面的铅直高度和水平距...