解直角三角形复习课件VIP免费

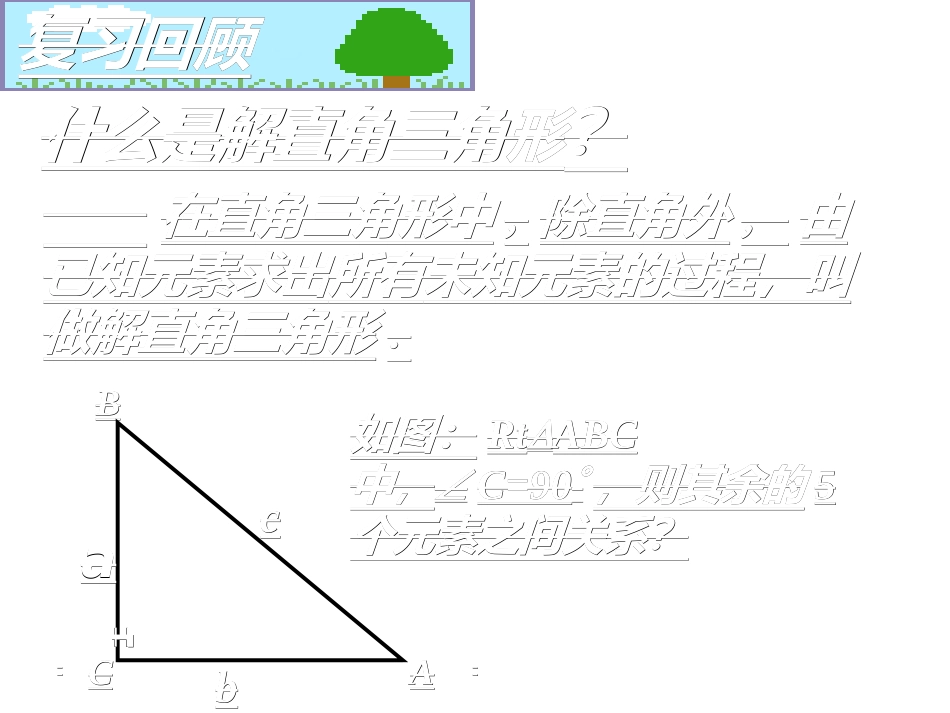
怀远县火庙中学崔伟怀远县火庙中学崔伟什么是解直角三角形什么是解直角三角形？？如图：如图：RtRtABCABC中，中，C=90C=90，则其余的，则其余的55个元素之间关系？个元素之间关系？复习回顾复习回顾在直角三角形中在直角三角形中,,除直角外除直角外,,由由已知元素求出已知元素求出所有所有未知元素的过程，叫未知元素的过程，叫做解直角三角形做解直角三角形..CCAABBbbccaa┏┏在在RtABC△RtABC△中，∠中，∠CC为直角，∠为直角，∠AA、∠、∠BB为锐角，为锐角，它们所对的边分别为它们所对的边分别为cc、、aa、、bb，其中除直角，其中除直角CC外，外，其余的其余的55个元素之间有以下关系：个元素之间有以下关系：⑴⑴三边之间的关系：三边之间的关系：222cba⑵⑵锐角之间的关系：锐角之间的关系：090BA⑶⑶边角之间的关系：边角之间的关系：;tan,cos,sinbaAcbAcaA.tan,cos,sinabBcaBcbBAABBbbaacc┏┏CC这些关系式中，每个关系式都包含这些关系式中，每个关系式都包含元素，知其中元素，知其中元素就可以求出元素就可以求出三个三个两个两个第三个元素第三个元素解直角三角形的依据解直角三角形的依据在在RtABC△RtABC△中，∠中，∠C=90°C=90°：：⑴⑴已知∠已知∠AA、、cc,,则则aa=__________;=__________;bb=_________=_________。。⑵⑵已知∠已知∠AA、、bb,,则则aa=__________;=__________;cc==。。⑶⑶已知∠已知∠AA、、aa，则，则bb=__________;=__________;cc==。。⑷⑷已知已知aa、、bb，则，则cc=__________=__________。。⑸⑸已知已知aa、、cc，则，则bb=__________=__________。。AABBbbaacc┏┏CC⌒⌒对边对边邻边邻边斜边斜边已知一锐角、斜边，求对边，用锐角的正弦；已知一锐角、斜边，求对边，用锐角的正弦；求邻边，用锐角的余弦。求邻边，用锐角的余弦。已知一锐角、邻边，求对边，用锐角的正切；已知一锐角、邻边，求对边，用锐角的正切；求斜边，用锐角的余弦。求斜边，用锐角的余弦。已知一锐角、对边，求邻边，用锐角的余切；已知一锐角、对边，求邻边，用锐角的余切；求斜边，用锐角的正弦。求斜边，用锐角的正弦。AcsinAccosAbtanAbcosAacotAasin22ba22ac解直角三角形的基本类型解直角三角形的基本类型::解直角三角形的方法解直角三角形的方法1.“1.“有斜用弦，无斜用切，宁乘毋除，取原避中有斜用弦，无斜用切，宁乘毋除，取原避中””意即意即::有斜边则用正、余弦，无斜边用正、余切，能用有斜边则用正、余弦，无斜边用正、余切，能用乘法计算时尽量不用除法计算，若既可用已知数据也可乘法计算时尽量不用除法计算，若既可用已知数据也可用中间过程得出数据时，则取“原始”，而不用“中间用中间过程得出数据时，则取“原始”，而不用“中间数据”。数据”。2.“2.“非转直”非转直”意即：对于非直角三角形的图形，可添加适当的辅意即：对于非直角三角形的图形，可添加适当的辅助线把它们分割成直角三角形或矩形来计算。助线把它们分割成直角三角形或矩形来计算。在解直角三角形及应用时在解直角三角形及应用时经常接触到的一些概念经常接触到的一些概念::（（11）仰角和俯角）仰角和俯角::（（22）方位角）方位角::30304545BBOOAA东东西西北北南南俯角俯角水平线水平线铅垂铅垂线线仰仰角角视线视线视线视线（（33）坡度）坡度::lhihl)(tan为坡角或倾斜角i11、小华同学去坡度为、小华同学去坡度为11︰︰22的土坡上种树，要求株距的土坡上种树，要求株距((相邻两树相邻两树间的水平距离间的水平距离))是是4m4m，斜坡上相邻两，斜坡上相邻两树间的坡面距离为树间的坡面距离为_____m_____mAABBCC251:21:24m4m22、“卡努”台风将一棵大树刮断、“卡努”台风将一棵大树刮断,,经测量，大树刮断一端的着地点经测量，大树刮断一端的着地点AA到树根部到树根部CC的距离为的距离为44米，倒下部分米，倒下部分ABAB与地平面与地平面ACAC的夹的夹角为角为45°45°，则这棵大树高是，则这棵大树高是米米..454544米米4246060““卡努”台风将一棵大树刮断，卡努”台风将一棵大树刮断，已知大...