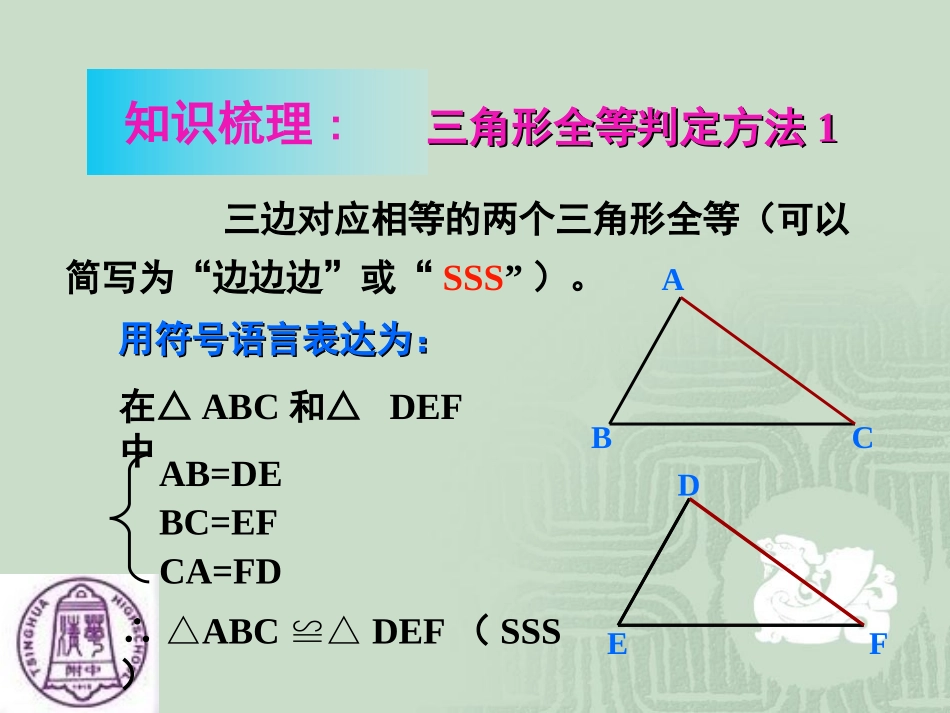
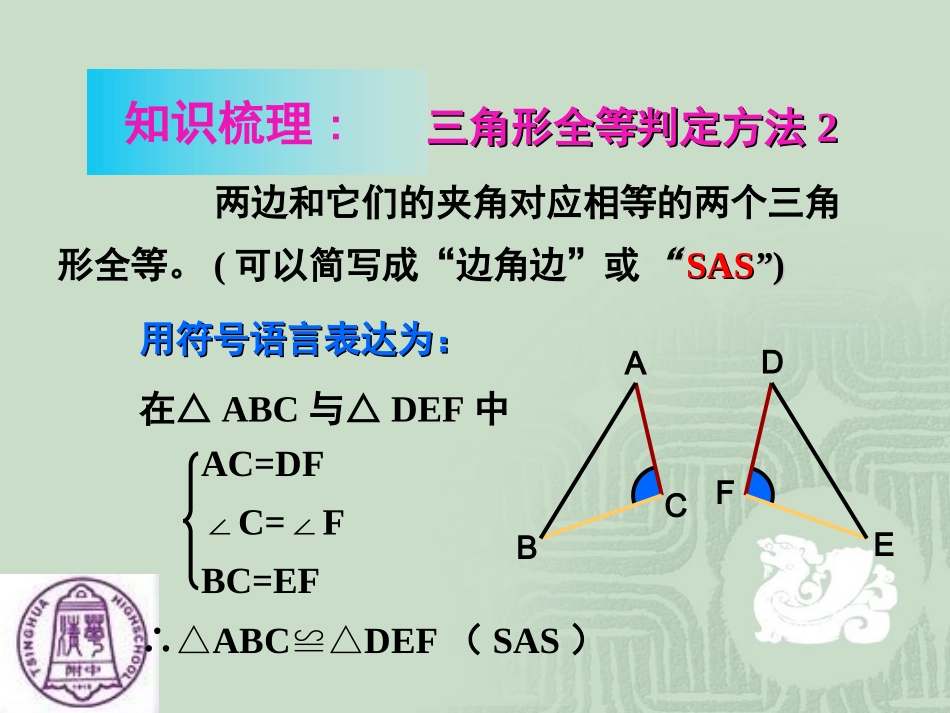
全等三角形复习中考版三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。ABCDEF在△ABC和△DEF中∴△ABCDEF≌△(SSS)AB=DEBC=EFCA=FD用符号语言表达为:用符号语言表达为:三角形全等判定方法三角形全等判定方法11知识梳理:三角形全等判定方法三角形全等判定方法22用符号语言表达为:用符号语言表达为:在△ABC与△DEF中∴△ABCDEF≌△(SAS)两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或““SASSAS””))知识梳理:FEDCBAAC=DF∠C=F∠BC=EF∠A=D∠(已知)AB=DE(已知)∠B=E∠(已知)在△ABC和△DEF中∴△ABCDEF≌△(ASA)有两角和它们夹边对应相等的两个三角有两角和它们夹边对应相等的两个三角形全等形全等((可以简写成“角边角”或“可以简写成“角边角”或“ASAASA””)。)。用符号语言表达为:用符号语言表达为:FEDCBA三角形全等判定方法三角形全等判定方法33知识梳理:知识梳理:思考思考:在△ABC和△DFE中,当∠A=D,C=F∠∠∠和AB=DE时,能否得到△ABCDFE?≌△三角形全等判定方法三角形全等判定方法44有两角和其有两角和其中一个角的对边对应相中一个角的对边对应相等的两个三角形全等等的两个三角形全等((可以简写成“角可以简写成“角边角”或“边角”或“AASAAS””)。)。CBAFED知识梳理:DCBAABDABCABDABCSSASSA不不能判定全能判定全等等典型例题:例例1(20061(2006浙江浙江):):如图如图,,点点BB在在AEAE上上,CAB=DAB,∠∠,CAB=DAB,∠∠要使要使ΔABCΔABD,≌ΔABCΔABD,≌可补充可补充的一个条件是的一个条件是..EDCBA分析:现在我们已知分析:现在我们已知AA→CAB=DAB∠∠→CAB=DAB∠∠①①用用SAS,SAS,需要补充条需要补充条件件AD=AC,AD=AC,②②用用ASA,ASA,需要补充条需要补充条件件∠∠CBA=DBA,∠CBA=DBA,∠③③用用AAS,AAS,需要补充条需要补充条件件∠∠C=D,∠C=D,∠④④此外此外,,补充条件补充条件∠∠CBCBE=DBE∠E=DBE∠也可以也可以(?)(?)SASSASASAASAAASAASSS→AB=AB(→AB=AB(公共边公共边).).AB=ACAB=AC∠∠CBA=DBA∠CBA=DBA∠∠∠C=D∠C=D∠∠∠CBE=DBE∠CBE=DBE∠典型例题:例例2(20062(2006湖南株洲湖南株洲):):如图如图,AE=AD,,AE=AD,要使要使ΔAΔABDΔACE,≌BDΔACE,≌请你增加请你增加一个条件是一个条件是..EDCBA分析分析::现在我们已知现在我们已知SS→AE=AD→AE=AD①①用用SAS,SAS,需要补充条需要补充条件件AB=AC,AB=AC,②②用用ASA,ASA,需要补充条需要补充条件件∠∠ADB=AEC,∠ADB=AEC,∠③③用用AAS,AAS,需要补充条需要补充条件件∠∠B=C,∠B=C,∠④④此外此外,,补充条件补充条件∠∠BDBDC=BEC∠C=BEC∠也可以也可以(?)(?)SASSASASAASAAASAAS(CD=BE(CD=BE行吗行吗?)?)AA→A=A(∠∠→A=A(∠∠公共角公共角).).例例3(20063(2006湖北十堰湖北十堰):):如如图图,,已知∠已知∠1=2,AC=AD,∠1=2,AC=AD,∠增加下列条件增加下列条件:AB=AE,①:AB=AE,①BC=ED,C=D,②③∠∠④BC=ED,C=D,②③∠∠④B=E,∠∠B=E,∠∠其中能使其中能使ΔABCΔABCΔAED≌ΔAED≌的条件有的条件有()()个个.A.4B.3.A.4B.3C.2D.1C.2D.121EDCBA典型例题: ∠ ∠1=2(∠1=2(∠已知已知)∴)∴1+EAB∠∠1+EAB∠∠=2+EAB,∠∠=2+EAB,∠∠即∠即∠BAC=EAD∠BAC=EAD∠例例3(20063(2006湖北十堰湖北十堰):):如如图图,,已知∠已知∠1=2,AC=AD,∠1=2,AC=AD,∠增加下列条件增加下列条件:AB=AE,①:AB=AE,①BC=ED,C=D,②③∠∠④BC=ED,C=D,②③∠∠④B=E,∠∠B=E,∠∠其中能使其中能使ΔABCΔABCΔAED≌ΔAED≌的条件有的条件有()()个个.A.4B.3.A.4B.3C.2D.1C.2D.121EDCBA典型例题:在在ΔABCΔABC和和ΔAEDΔAED中中AC=ADAC=ADBAC=EAD∠∠BAC=EAD∠∠AB=AEAB=AE∴∴ΔABCΔAED(SAS)≌ΔABCΔAED(SAS)≌AB=AEAB=AE①①AB=AEAB=AE例例3(20063(2006湖北十堰湖北十堰):):如如图图,,已知∠已知∠1=2,AC=AD,∠1=2,AC=AD,∠增加下列条件增加下列条件::AB=AE①AB=AE①,,BC=ED,C=D,②③∠∠④BC=ED,C=D,②③∠∠④B=E,∠∠B=E,∠∠其中能使其中能使ΔABCΔABCΔAED≌ΔAED≌的条件有的条件有()()个个.A.4B.3.A.4B.3C.2D.1C.2D.121EDCBA典型例题:在在ΔABCΔABC...