定积分的应用VIP免费

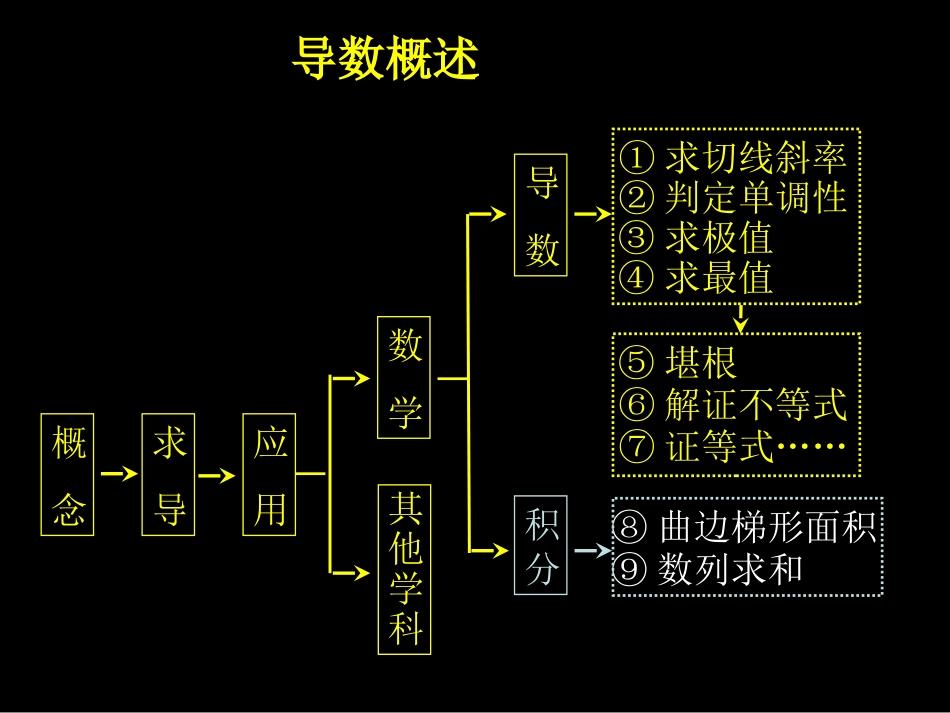
§223定积分的应用二、定积分在运动学中的应用：一、定积分在数学中的应用：三、定积分在力学中的应用：位移速度加速度跃度功力1.曲边图形的面积2.数列求和3.平面曲线的弧长4.旋转体的体积概念导数概述求导应用数学其他学科导数积分①求切线斜率②判定单调性③求极值④求最值⑤堪根⑥解证不等式⑦证等式……⑨数列求和⑧曲边梯形面积割线极限是切线一导本身是斜率必须切点横坐标切点坐标及斜率知一有二基本功在即切点过待定bkxy00)(00xfy10100/)(xxyyxfk),(000yxP),(111yxP导数的几何意义二导意义是曲率大凹小凸○拐点导数法判定单调性第一确定定义域第二求导到显然注1：最终结果要显然乘积配方与○比注2：增大减小○驻点等号问题待大学含参反用必须等其他情况暂忽略注3：书写格式要简明三解不等得结论书写格式要简明①②③①当f(x)单调时②当f(x)不单调时因在Domain上恒成立0)(xf故f(x)在Domain上↗（↘）0)(xf当xDomain∈时，解得f(x)在I1，I2…上↗当xDomain∈时，解得f(x)在I1，I2…上↘0)(xf2.二导法求极值：一求驻点二筛选大小小大○为非一般地，若f(x0)是极小值0)(0/xf则0)(0//xf0)(0//xf0)(0//xff(x0)是极大值f(x0)是非极值①②③1.一导法求极值：一求驻点二单调三写极值靠图象书写格式要简明含参反用须验根二、数法：一、形法：顶点即是极值点谷底极小峰极大极值的求法最值的求法1.形法2.数法函数图象线性规划函数法(单调性法)最值定理必有最值闭且连最值来源顶端点导数法——单调性法的特例看图说话是关键最值来源顶端点一论单调算顶端三写最值是格式能代则代罗比达是则名为筛选法§223定积分的应用二、定积分在运动学中的应用：一、定积分在数学中的应用：三、定积分在力学中的应用：位移速度加速度跃度功力1.曲边图形的面积2.数列求和3.平面曲线的弧长4.旋转体的体积一、定积分在数学中的应用：1.曲边图形的面积S1：画简图：S3：求交点：S2：巧分割：S4：写式子：即求积分上下限能整勿碎整体性充分利用对称性积分变量方向性灵活应用割补法求曲边图形的面积五大步骤S5：算面积：S1：画简图(0,0)(1,1)OB32130233()xx.31-OABDOABCSSS梯曲形曲梯形11200xdxxdx201yxxxyx及oxy2yx2yxABCD(1)课本P：56例1练习1.求曲边图形的面积：S3：求交点：S2：巧分割：S4：写式子：S5：算面积：120(-)Sxxdx或120(-)Sxxdx或(2)课本P：57例2S1：画简图S3：求交点：S2：巧分割：S4：写式子：S5：算面积：2yx4yxS1S2(0,0),(8,4).24yxyx8440)]4(2[2dxxxdxxS3828204221404323|()|xxx法1：(2)课本P：57例2S1：画简图S3：求交点：S2：巧分割：S4：写式子：S=S5：算面积：(0,0),(8,4).24yxyx法2：S138202283|x2240162833(2)课本P：57例2S1：画简图S3：求交点：S2：巧分割：S4：写式子：S=S5：算面积：(0,0),(8,4).24yxyx法3：212xy4xy234011426()|yyy23114044442634201432[()]syydy法：S1：画简图S2：巧分割：法1：(3)计算由曲线xy22和直线4xy所围成的图形的面积xy224xy1S2SS1：画简图S2：巧分割：法2：(3)计算由曲线xy22和直线4xy所围成的图形的面积xy224xy1S2S1SS1：画简图S2：巧分割：法3：(3)计算由曲线xy22和直线4xy所围成的图形的面积xy224xy1SS1：画简图S2：巧分割：法4：(3)计算由曲线xy22和直线4xy所围成的图形的面积xy224xy1SS1：画简图S3：求交点：S2：巧分割：S4：写式子：S=S5：算面积：法5：(3)计算由曲线xy22和直线4xy所围成的图形的面积212xy4xy).4,8(),2,2(422xyxy234211426()|yyy18(4)课本P：58练习12131425(5)如图,曲线y=x2经过正方形OABC的顶点B，现将一质点随机投入正方形，则质点落在图中阴影区域内的概率是(A)(B)(C)(D)10123011xdxx.33OABC1S13P.S13阴影概率析:S阴影=一、定积分在数学中的应用：1.曲边图形的面积2.数列求和3.平面曲线的弧长4....