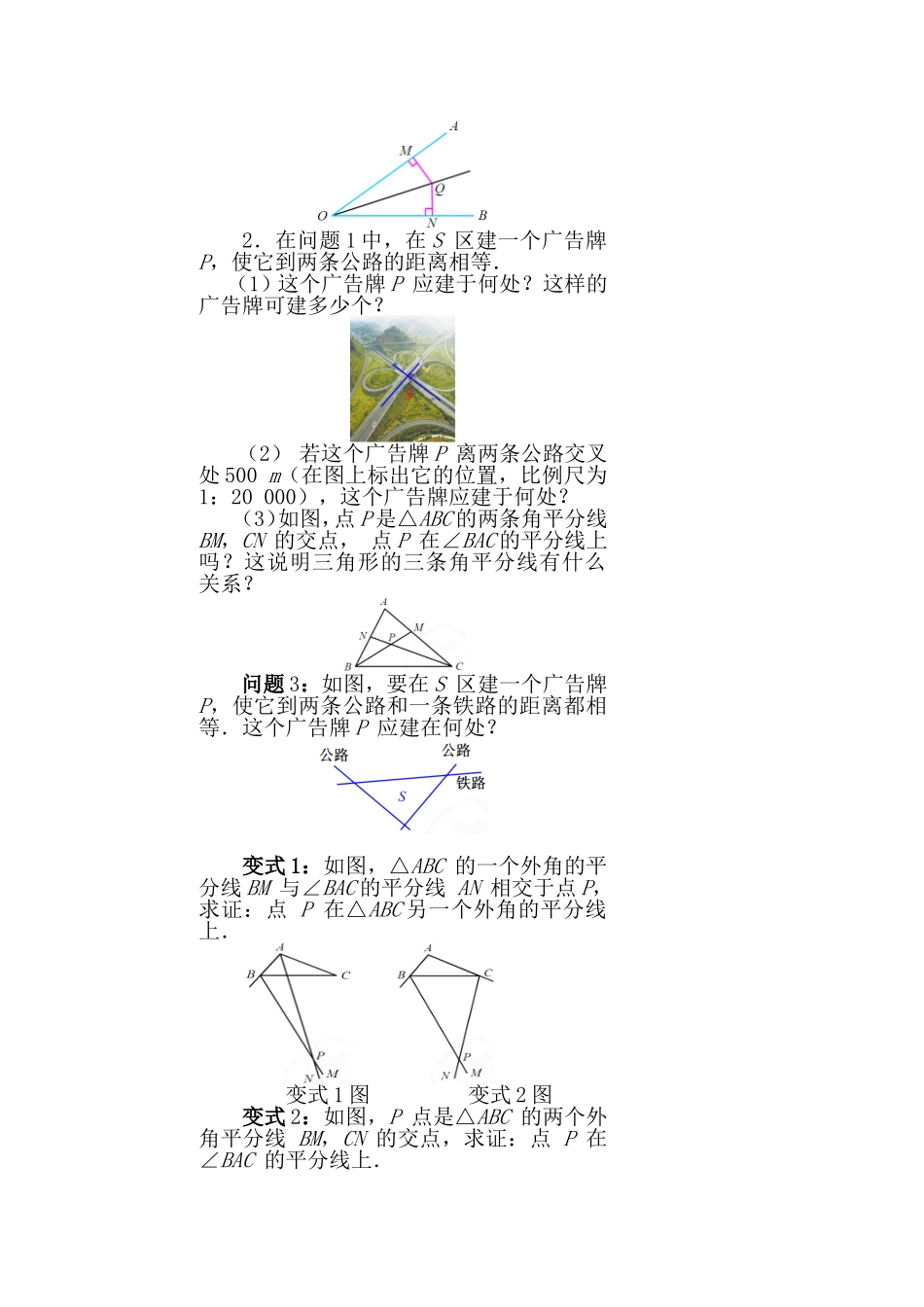
课题:§12.3.1角平分线的性质(2)课标要求探索并证明角平分线的性质的逆定理:角的内部到角两边距离相等的点在角的平分线上.教学目标知识技能掌握角平分线性质的逆定理,并能利用这些方法解决简单的数学问题和实际问题.数学思考经历探究角平分线性质逆定理的过程,发展学生合情推理能力和演绎推理力.解决问题了解角平分线性质在生活、生产中的应用,进一步发展学生的推理证明意识和能力.情感态度结合实际,创造丰富的情境,提高学生的学习兴趣,让他们在活动中获得成功的体验,培养学生的探索精神,树立学习的信心.重点角平分线性质和判定的应用.难点运用角平分线性质和判定证明及解决实际问题.学情分析通过上节课的学习,学生已掌握角平分线的性质,本节是在此基础之上,并利用学生学习的全等的知识来探究角平分线性质定理的逆定理.教法演示、探究、讨论学法动手操作、合作学习教具圆规、三角板教学程序设计教学环节教学内容二次备课一、情境引入引入:问题1:如图,要在S区建一个广告牌P,使它到两条高速公路的距离相等,离两条公路交叉处500m,请你帮忙设计一下,这个广告牌P应建于何处(在图上标出它的位置,比例尺为1:20000)?二、探索发现探索并证明角平分线的性质定理的逆定理问题2:交换角的平分线的性质中的已知和结论,你能得到什么结论,这个新结论正确吗?角的内部到角的两边距离相等的点在角的平分线上.追问1:你能证明这个结论的正确性吗?追问2:这个结论与角的平分线的性质在应用上有什么不同?强调:这个结论可以判定角的平分线,而角的平分线的性质可用来证明线段相等.教学环节教学内容三、应用提高应用角平分线性质定理的逆定理1.判断题:(1)如图,若QM=QN,则OQ平分∠AOB;(2)如图,若QM⊥OA于M,QN⊥OB于N,则OQ是∠AOB的平分线;(3)已知:Q到OA的距离等于2cm,且Q到OB距离等于2cm,则Q在∠AOB的平分线上.2.在问题1中,在S区建一个广告牌P,使它到两条公路的距离相等.(1)这个广告牌P应建于何处?这样的广告牌可建多少个?(2)若这个广告牌P离两条公路交叉处500m(在图上标出它的位置,比例尺为1:20000),这个广告牌应建于何处?(3)如图,点P是△ABC的两条角平分线BM,CN的交点,点P在∠BAC的平分线上吗?这说明三角形的三条角平分线有什么关系?问题3:如图,要在S区建一个广告牌P,使它到两条公路和一条铁路的距离都相等.这个广告牌P应建在何处?变式1:如图,△ABC的一个外角的平分线BM与∠BAC的平分线AN相交于点P,求证:点P在△ABC另一个外角的平分线上.变式1图变式2图变式2:如图,P点是△ABC的两个外角平分线BM,CN的交点,求证:点P在∠BAC的平分线上.变式3:如图,将问题3中“S区”去掉,广告牌P到两条公路和一条铁路的距离相等.这个广告牌P应建在何处?四、巩固练习课堂练习课本P51页习题12.3第4、5题五、体验收获谈谈你的收获和体会六、实践延伸课后作业:课本P51页习题12.3第3、7题附:板书设计§12.3.2角平分线的性质(2)一、角平分线性质的逆定理:角的内部到角的两边距离相等的点在角的平分线上.例题板演区学生板演区