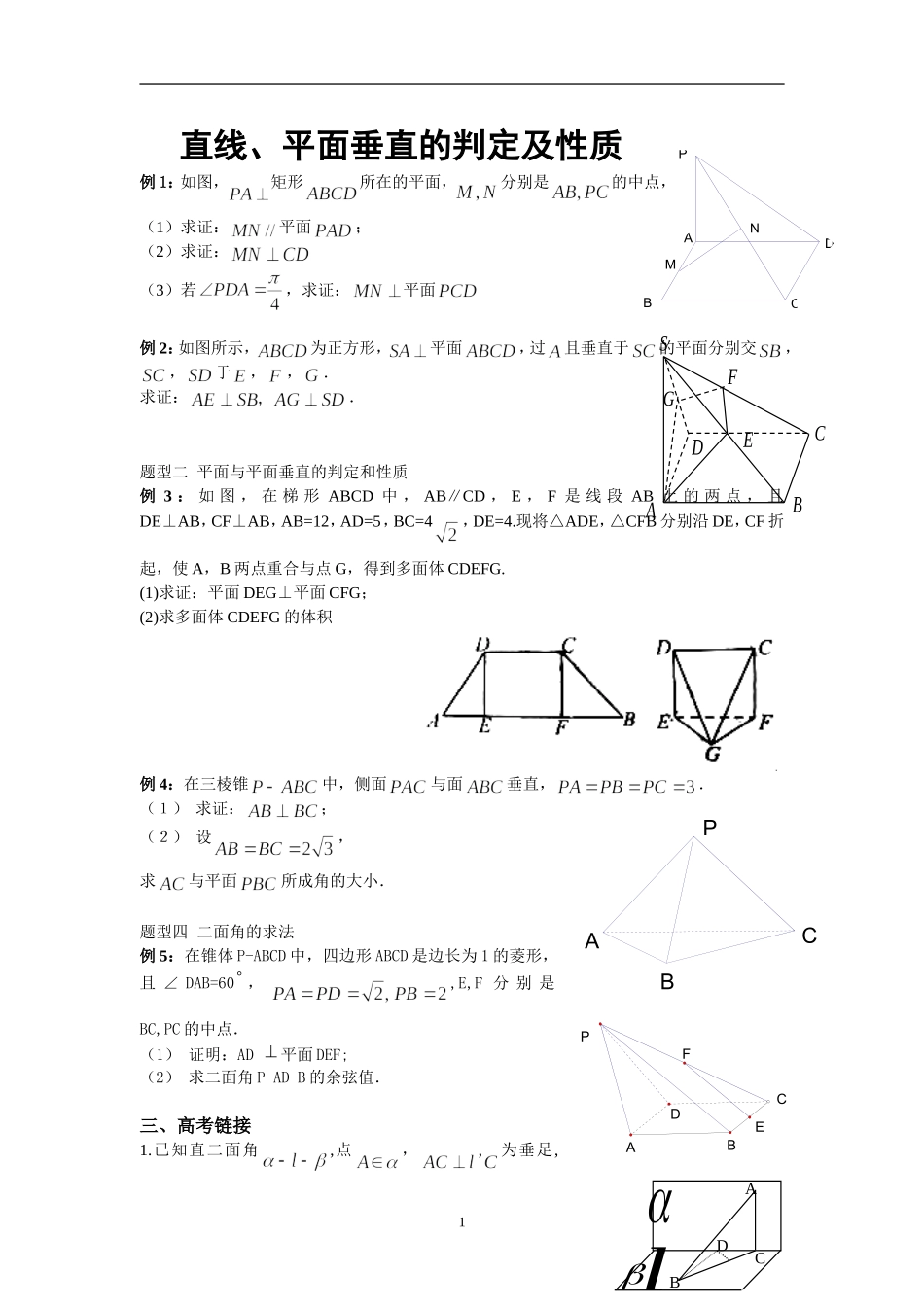
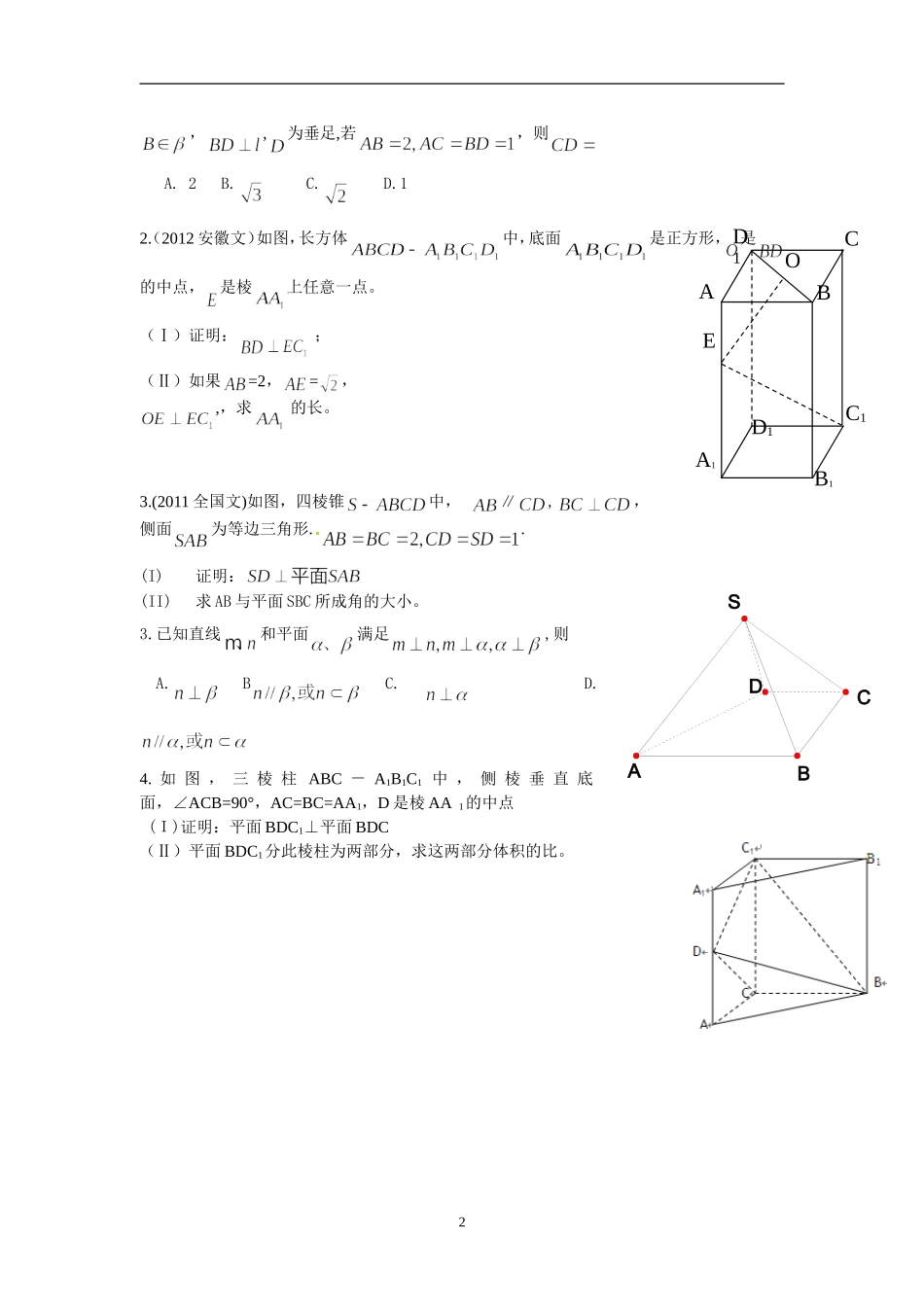
ClABDNMPDCBASABCFEDG直线、平面垂直的判定及性质例1:如图,矩形所在的平面,分别是的中点,(1)求证:平面;(2)求证:(3)若,求证:平面例2:如图所示,为正方形,平面,过且垂直于的平面分别交,,于,,.求证:.题型二平面与平面垂直的判定和性质例3:如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.(1)求证:平面DEG⊥平面CFG;(2)求多面体CDEFG的体积例4:在三棱锥中,侧面与面垂直,.(1)求证:;(2)设,求与平面所成角的大小.题型四二面角的求法例5:在锥体P-ABCD中,四边形ABCD是边长为1的菱形,且∠DAB=60,,E,F分别是BC,PC的中点.(1)证明:AD平面DEF;(2)求二面角P-AD-B的余弦值.三、高考链接1.已知直二面角,点,,为垂足,1DFCEBAPABCP,,为垂足,若,则A.2B.C.D.12.(2012安徽文)如图,长方体中,底面是正方形,是的中点,是棱上任意一点。(Ⅰ)证明:;(Ⅱ)如果=2,=,,,求的长。3.(2011全国文)如图,四棱锥中,∥,,侧面为等边三角形..(I)证明:(II)求AB与平面SBC所成角的大小。3.已知直线和平面满足,则A.BC.D.4.如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=AA1,D是棱AA1的中点(I)证明:平面BDC1⊥平面BDC(Ⅱ)平面BDC1分此棱柱为两部分,求这两部分体积的比。2AOCD1ED1BC1A1B1DCASB8.如图6,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD。(Ⅰ)证明:BD⊥PC;(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积。3