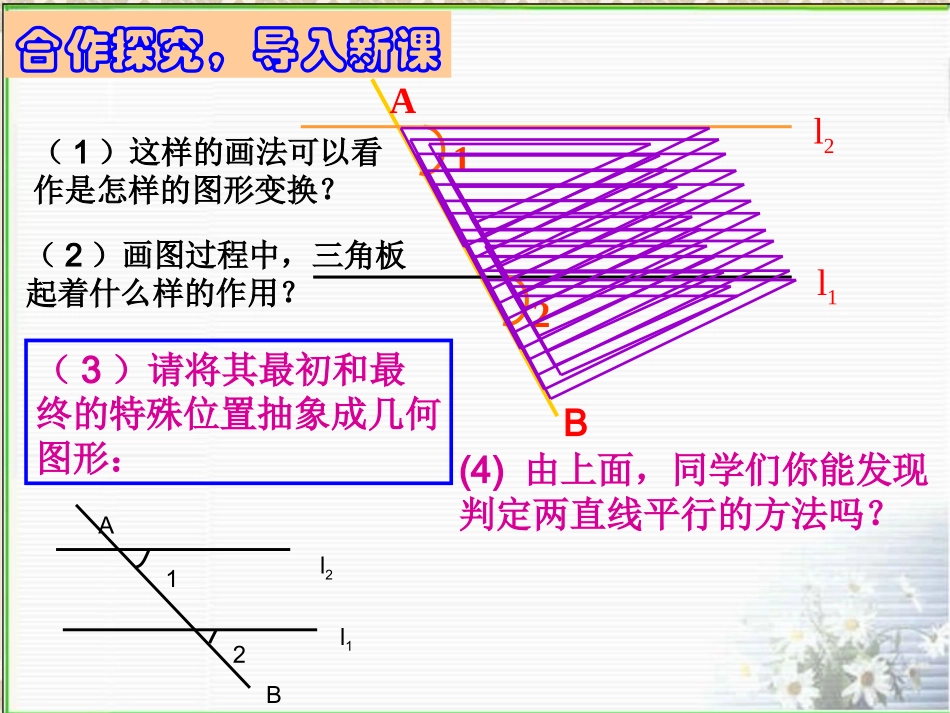
预习检测:预习检测:预习课本P12-14,解决以下几个问题:1.通过预习回答P12“思考”中提到的问题:我们在用直尺和三角尺画平行线的过程中,三角尺起到什么样的作用?2.平行线的判定定理分别是什么?3.自主学习,完成课本P14练习题1和2合作探究,导入新课l1A21l2B(1)这样的画法可以看作是怎样的图形变换?(3)请将其最初和最终的特殊位置抽象成几何图形:12l2l1AB(2)画图过程中,三角板起着什么样的作用?(4)由上面,同学们你能发现判定两直线平行的方法吗?两条直线被第三条所截,如果同位角相等,那么这两条直线平行.简单地说:同位角相等,两直线平行.平行线的判定平行线的判定(1):(1):1=2(已知)------//------()12l2l1AB几何语言l2l1同位角相等,两直线平行同位角相等,两直线平行下图中,如果∠2=3∠,能得出AB∥CD吗?写出你的推理过程数学推理的魅力解:2=3∵∠∠∠1=3∠∴∠1=2∠∴ABCD∥B3ACDF12E()已知()对顶角相等()等量代换()同位角相等两直线平行两直线平行的判定方法(2):两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单地说:内错角相等,两直线平行.B32ADEFC几何语言∵2=3(已知)∴AB//CD(内错角相等,两直线平行)做一做001120,2120,03120,证明:∵﹙已知﹚即:∠1=2∠∴﹙内错角相等,两直线平行﹚001120,2120,21//ll同理:∵∠2=3=120°∠﹙已知﹚∴﹙同位角相等,两直线平行﹚34//ll如图,已知说出其中的平行线,并说明理由.例1:2l1l4l3l123下图中,如果∠4+2=180∠°,能得出AB∥CD?解:4+2=180°∵∠∠(已知)∠4+1=180°∠(邻补角的定义)∴∠2=1∠(同角的补角相等)∴ABCD∥(同位角相等,两直线平行)3AC142DBEF你还有其它的说理方法吗?数学推理的魅力两直线平行的判定(3):两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单地说:同旁内角互补,两直线平行.2BACDEF4几何语言∵2+4=180°(已知)∴AB//CD(内错角相等,两直线平行)下图中,如果∠4+2=180∠°,能得出AB∥CD?3AC1425DBEF解∵∠4+2=180°∠(已知)∠4+3=180°∠(邻补角的定义)∴∠2=3∠(同角的补角相等)∴ABCD∥(内错角相等,两直线平行)数学推理的魅力1.如图,(1)从∠1=2∠,可以推出∥理由是(2)从∠2=∠,可以推出c∥d,理由是(3)如果∠4=75°,∠3=75°,可以推出∥(4)从∠4=75°,∠5=°,可以推出a∥b.考考你dba内错角相等,两直线平行同位角相等,两直线平行.33ab1254cdc1052.如图:直线AB、CD都和AE相交,且∠1+∠A=180º.求证:AB//CDCBAD21E证明:∵∠1+∠A=180º3练习练习∴∠2+∠A=180º∴()()()()已知对顶角相等等量代换同旁内角互补,两直线平行∠1=2∠ABCD∥o3.小明用如图所示的方法作出了平行线,你认为他的作法对吗?为什么?内错角相等,两直线平行内错角相等,两直线平行平行线的判定?判定定理1:同位角相等,两直线平行.∵∠1=2,∠∴a∥b.判定定理2:内错角相等,两直线平行.∵∠3=42,∠∴a∥b.几何语言☞☞判定定理3:同旁内角互补,两直线平行.∵∠5+6=180∠0,∴a∥b.abc21abc34abc56这里的结论,以后可以直接运用.1.同位角相等,两直线平行.2.内错角相等,两直线平行.3.同旁内角互补,两直线平行.4.如果两条直线都与第三条直线平行,那么这两条直线也互相平行.5.平行线的定义:同一平面内,没有交点的两直线平行.可用来判定两条直线是否平行的方法有:课后作业:P15.第2(画一个简图)、4题预习作业:预习课本P14,“探究”并理解探究下面的例题